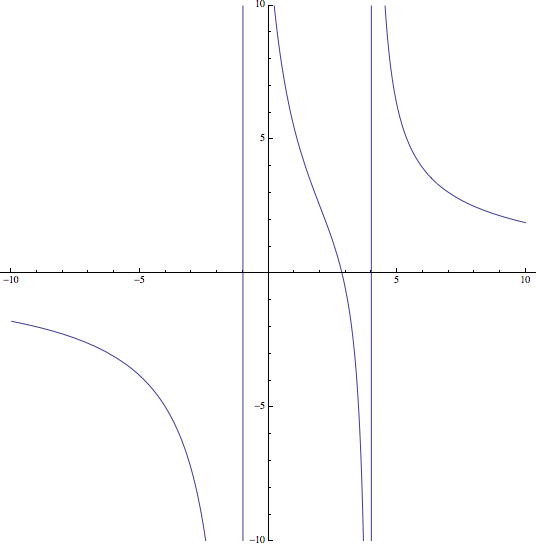
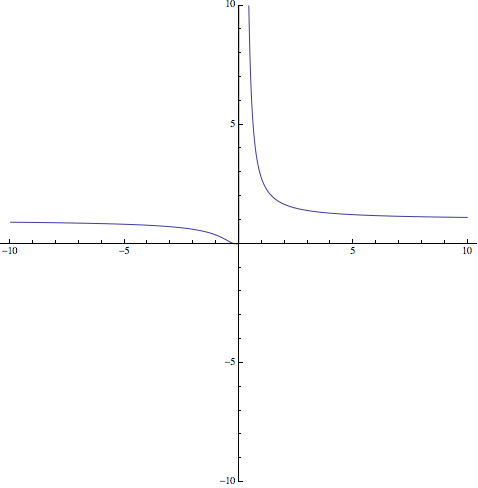
Ejercicio : (Septiembre 2013 Opción A) (Calificación: 3 ptos)
Dada la función \(f(x)=\frac{4}{x-4}+\frac{27}{2x+2}\)
Se pide:
a) (0,75 ptos) Hallar las asíntotas de su gráfica
b) (1,75 ptos) Determinar los intervalos de crecimiento y decrecimiento y calcular sus puntos de inflexión
c) (0,5 ptos) Esbozar la gráfica de la función
a) Para estudiar las asintótas de la función, consultar el apartado de teoría de asíntotas
. Asintótas verticales:
Las posibles asíntotas verticales estarían en los puntos que no están en el dominio, ver cómo se calcula el dominio de una función. En este caso, los denominadores se anulan en \(x=4\) y \(x=-1\), consultando cómo resolver límites, se tiene
\(\lim\limits_{x\to -1^{-}}\frac{4}{x-4}+\frac{27}{2x+2}=-\infty\)
\(\lim\limits_{x\to -1^{+}}\frac{4}{x-4}+\frac{27}{2x+2}=\infty\)
Luego, hay una asíntota vertical en \(\bbox[yellow]{x=-1}\)
Por otra parte,
\(\lim\limits_{x\to 4^{-}}\frac{4}{x-4}+\frac{27}{2x+2}=-\infty\)
\(\lim\limits_{x\to 4^{+}}\frac{4}{x-4}+\frac{27}{2x+2}=\infty\)
De manera que hay otra asíntota vertical en \(\bbox[yellow]{x=4}\)
. Asintótas horizontales:
Consultando cómo se resuelven límites, se tiene que
\(\lim\limits_{x\to\pm\infty}\frac{4}{x-4}+\frac{27}{2x+2}=\lim\limits_{x\to\pm\infty}\frac{5(7x-20)}{2(x^2-3x-4)}=\lim\limits_{x\to\pm\infty}\frac{7x}{x^2}=0\)
Luego, hay una asíntota horizontal en \(\bbox[yellow]{y=0}\)
. Asintótas oblicuas:
Las posibles asíntotas oblicuas tendrían la siguiente expresión \(y=mx+n\)
Pero como hay asíntotas horizontales, no puede haber asíntotas oblicuas, luego \(\bbox[yellow]{\hbox{no hay}}\)
b) Los intervalos de crecimiento y decrecimiento se estudiarán calculando los máximos y mínimos de la función, ver máximos y mínimos, la tabla de derivadas y consultar también cómo resolver polinomios
\(f'(x)=\frac52\frac{-7x^2+40x-88}{(x^2-3x-4)^2}=0\Rightarrow 7x^2-40x+88=0\Rightarrow x=\frac{40\pm\sqrt{-864}}{14}\) que no está en \(\mathbb{R}\)
Por lo tanto, no habrá máximos ni mínimos
Para hallar los puntos de inflexión de \(f(x)\), se estudia la curvatura de la función, para ello se iguala la segunda derivada a cero (hallada en el apartado anterior), ver cómo estudiar la curvatura de una función y consultar también cómo resolver polinomios
\(f»(x)=5\frac{7x^3-60x^2+264x-344}{(x^2-3x-4)^3}=0\Rightarrow 7x^3-60x^2+264x-344=0\)
Utilizando la Regla de Ruffini se resuelve el polinomio, obteniendo la única raíz real \(x=2\), luego, el punto de inflexión será \(\bbox[yellow]{(2,-\frac{31}{2})}\)
Para saber cómo cambia la curvatura de la función, se evalúa el signo de la segunda derivada antes y después del punto obtenido y antes y después de la asíntotas verticales obtenidas \(x=-1\) y \(x=4\)
Se tiene que la función en \((-\infty,-1)\) y de \((2,4)\) será convexa, y en el intervalo \((-1,2)\) y en el \((4,\infty)\) será cóncava
c) Para representar la función se seguirán los pasos para dibujar el gráfico de una función
– El dominio en este caso serán todos los números reales menos \(\{-1,4\}\) ya que los denominadores se anulan en esos valores, ver dominio de una función
– Para calcular el corte con los ejes se iguala la función a cero, ver cómo obtener los cortes con los ejes
\(f(x)=0\Rightarrow x=\frac{20}{7}\), luego la función cortará a \(y=0\) en \(x=\frac{20}{7}\)
Por otra parte, evaluando \(f(0)\) se tiene \(f(0)=\frac{100}{8}\), luego otro punto de corte será \((0,\frac{100}{8})\)
Con estos datos y los obtenidos en los apartados anteriores, es posible dibujar la función
Ejercicio : (Septiembre 2013 Opción B) (Calificación:2 ptos)
Dada la función \(f(x)=e^{\frac{1}{x}}\), se pide:
se pide:
a) (1 pto) Calcular \(\lim\limits_{x\to\infty}f(x)\), \(\lim\limits_{x\to -\infty}f(x)\) y estudiar la existencia de \(\lim\limits_{x\to 0}f(x)\)
b) (1 pto) Esbozar la gráfica \(y=f(x)\) determinando los intervalos de crecimiento y decrecimiento de \(f(x)\) y sus asíntotas
a) Para estudiar los límites, recordar la teoría de cómo resolver límites
\(\lim\limits_{x\to\infty}f(x)= \lim\limits_{x\to\infty}e^{\frac 1x}=e^{\frac{1}{\infty}}=1\) y \(\lim\limits_{x\to -\infty}f(x)= \lim\limits_{x\to -\infty}e^{\frac 1x}=e^{\frac{1}{-\infty}}=1\)
Para estudiar la existencia de \(\lim\limits_{x\to 0}f(x)\), se estudian los límites laterales y se comprueba que, si existen, son iguales, ver teoría de límites y derivabilidad
En este caso se tiene \(\lim\limits_{x\to 0^{-}}f(x)=\lim\limits_{x\to 0^{-}}e^{\frac 1x}=0\)
Por otra parte, \(\lim\limits_{x\to 0^{+}}f(x)=\lim\limits_{x\to 0^{+}}e^{\frac 1x}=\infty\)
Luego, \(\lim\limits_{x\to 0^{-}}f(x)\neq\lim\limits_{x\to 0^{+}}f(x)\Rightarrow\bbox[yellow]{\hbox{no existe }\lim\limits_{x\to 0}f(x)}\)
b) Los intervalos de crecimiento y decrecimiento se estudiarán calculando los máximos y mínimos de la función, ver máximos y mínimos y la tabla de derivadas
\(f'(x)=e^{\frac 1x}\frac{-1}{x^2}=-\frac{e^{\frac 1x}}{x^2}\neq 0\), luego, no hay puntos críticos y \(f'(x)\) es siempre menor que cero, luego la función \(\bbox[yellow]{\hbox{es decreciente en todo su dominio}}\)
Para estudiar las asintótas de la función, consultar el apartado de teoría de asíntotas
. Asintótas verticales:
Las posibles asíntotas verticales estarían en los puntos que no están en el dominio, ver cómo se calcula el dominio de una función. En este caso, el único punto real en el que no está definida la función es el cero, luego el dominio serán todos los números reales menos el cero
Para comprobar si en este punto hay asíntota se calculan los límites laterales de la función. En este caso ya se han calculado en el primer apartado, por lo que se puede concluir que la función tiene una asíntota vertical \(\bbox[yellow]{\hbox{cuando } x\hbox{ se aproxima a cero por la derecha}}\)
. Asintótas horizontales:
Consultando el apartado anterior se tiene que \(\lim\limits_{x\to\pm\infty}f(x)=1\), luego hay una asíntota horizontal en \(\bbox[yellow]{y=1}\)
. Asintótas oblicuas:
Como hay asíntotas horizontales, \(\bbox[yellow]{\hbox{no hay oblicuas}}\), ver la teoría de asíntotas
-> Para representar la función se seguirán los pasos para dibujar el gráfico de una función:
– Como ya se ha comentado, el dominio en este caso serán todos los números reales menos el cero
– Para calcular el corte con los ejes se iguala la función a cero, ver cómo obtener los cortes con los ejes
\(f(x)=0\Rightarrow \hbox{Imposible}\), luego la función no cortará a \(y=0\)
Por otra parte, como \(x=0\) no está en el dominio, no se obtiene ningún punto de corte con el eje \(OY\)
Con estos datos y los obtenidos en los apartados anteriores, es posible dibujar la función
Ejercicio : (Septiembre 2013 Opción B) (Calificación: 2 ptos)
Dada la función: \(\displaystyle\frac{x}{x^2+1}\), se pide:
a) (1 pto) Hallar la ecuación de la recta tangente a la gráfica de la función en el punto de abscisas \(x=0\)
b) (1 pto) Calcular \(\displaystyle\int_0^1xf(x)dx\)
a) La ecuación de la recta tangente en \(x=0\) viene dada por la siguiente ecuación, ver ecuaciones de la recta
\(y-f(0)=f'(0)(x-0)\)
Primeramente se calculará \(f(0)=\frac{0}{0^2+1}=0\) y la derivada de la función, ver la tabla de derivadas
\(f'(x)=\displaystyle\frac{1(x^2+1)-x2x}{(x^2+1)^2}\)
Luego, \(f'(0)=\frac{1-0^2}{(0^2+1)^2}=1\)
Por lo tanto, se tendrá el resultado \(y-0=(x-0)\Rightarrow\bbox[yellow]{y=x}\)
b) Consultando la tabla de integrales y recordando cómo se resuelven integrales definidas, se tiene
\(\displaystyle\int_0^1xf(x)dx=\displaystyle\int_0^1 x\frac{x}{x^2+1}dx=\displaystyle\int_0^1 \frac{x^2}{x^2+1}dx\)
Dividiendo el numerador entre el denominador, se tiene
\(\displaystyle\int_0^1 \frac{x^2}{x^2+1}dx=\displaystyle\int_0^1 (1-\frac{1}{x^2+1})dx=\displaystyle\int_0^1 1dx-\displaystyle\int_0^1\frac{1}{x^2+1}dx=x\Big]_0^1-\arctan x\Big]_0^1=\bbox[yellow]{1-\frac{\pi}{4}}\)