Ejercicio : (Junio 2012 Opción B) (Calificación: 3 ptos)
Dada la función: \(f(x)=\displaystyle\begin{cases}x^2-4x+3&x\leq 1\\ -x^2+4x-3&x>1\\\end{cases}\)
a) (1 pto) Estúdiese la continuidad y la derivabilidad de la función \(f(x)\)
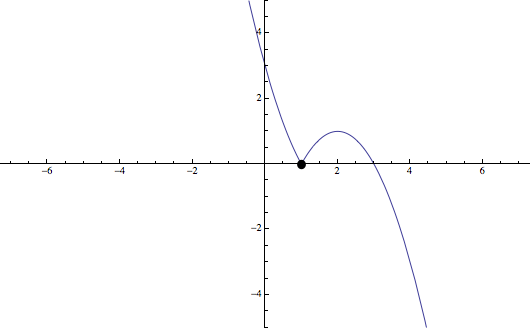
b) (1 pto) Represéntese gráficamente la función \(f(x)\)
c) (1 pto) Calcúlese el área del recinto plano acotado limitado por la gráfica de \(f(x)\), el eje \(OX\), el eje \(OY\) y la recta \(x=2\)
a) La función está formada por polinomios, luego el único punto de posible discontinuidad es el salto entre los polinomios, \(x=1\) (ver continuidad de funciones)
Para comprobar si la función es continua en dicho punto se evalúan los límites laterales y la función en el punto
\(\lim\limits_{x\to 1^{+}}f(x)=\lim\limits_{x\to 1^{+}}-x^2+4x-3=-1^2+4.1-3=0\)
Calculando el otro límite lateral, se tiene
\(\lim\limits_{x\to 1^{-}}f(x)=\lim\limits_{x\to 1^{-}}x^2-4x+3=0=f(1)\)
Luego, se cumple la condición de continuidad, luego \(\bbox[yellow]{f(x)\hbox{ es continua para todos los reales}}\)
Para que la función sea derivable tiene que cumplirse que \(f'(1^{-})=f'(1^{+})\), ver derivabilidad
En este caso, calculando primeramente la derivada de la función, se tiene
\(f'(x)=\displaystyle\begin{cases}2x-4&x\leq 1\\ -2x+4&x>1\\\end{cases}\)
Evaluando \(f'(1^{-})=f'(1^{+})\), se tiene que \(-2=2\Rightarrow \hbox{Imposible}\), luego, \(\bbox[yellow]{f(x) \hbox{ no es derivable en }x=1}\)
b) Para representar la función se seguirán los pasos para dibujar el gráfico de una función
– El dominio en este caso serán todos los números reales ya que está formada por dos polinomios, ver dominio de una función
– Para calcular el corte con los ejes se iguala la función a cero, ver cómo obtener los cortes con los ejes
\(f(x)=0\Rightarrow x^2-4x+3=0\) y \(-x^2+4x-3=0\), luego, consultando cómo resolver polinomios, se tienen las siguientes soluciones \(x=1\) y \(x=3\), luego la función cortará al eje \(OX\) en \((1,0)\) y en \((3,0)\) (ambos polinomios cortan al eje en esos puntos)
Por otra parte, evaluando \(f(0)\) se tiene \(f(0)=0^2-4.0+3=3\), luego otro punto de corte será \((0,3)\)
Con estos datos y sabiendo que ambos polinomios son parábolas trasladadas, recordar las funciones elementales es posible dibujar la función
c) Para hallar el área pedida y teniendo en cuenta la gráfica de la función \(f(x)\), los intervalos donde se define cada trozo de la función y la teoría de cómo se calcula una integral definida, se tiene
\(\displaystyle A=\int_0^{2}f(x)dx=\displaystyle\int_{0}^{1}(x^2-4x+3)dx+\int_1^2(-x^2+4x-3)dx=\frac{x^3}{3}-4\frac{x^2}{2}+3x\Big]_{0}^{1}-\frac{x^3}{3}+4\frac{x^2}{2}-3x\Big]_1^2=\frac 43-0+(-\frac 23)-(-\frac 43)=\bbox[yellow]{2}\)
Ejercicio : (Septiembre 2012 Opción A) (Calificación: 3 ptos)
Se considera la función real de variable real definida por \(f(x)=\frac{x(2x-1)}{x-1}\)
a) (1 pto) Determínense las asíntotas de \(f(x)\). Calcúlense los extremos relativos de \(f(x)\)
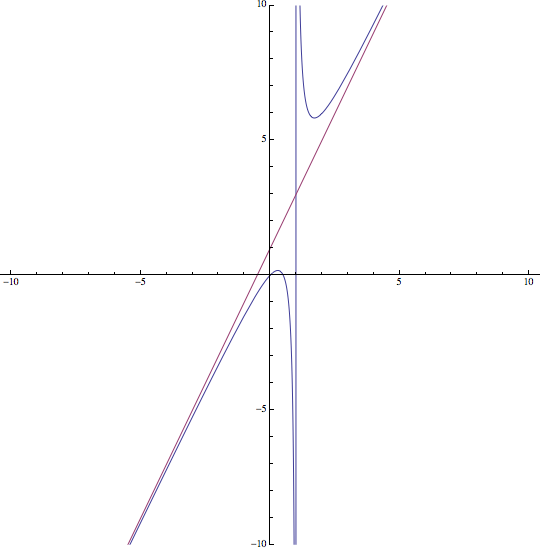
b) (1 pto) Represéntese gráficamente la funcón \(f(x)\)
c) (1 pto) Calcúlese \(\displaystyle\int_2^5\frac{f(x)}{x^2}dx\)
a) Para estudiar las asintótas de la función, consultar el apartado de teoría de asíntotas
. Asintótas verticales:
Las posibles asíntotas verticales estarían en los puntos que no están en el dominio, ver cómo se calcula el dominio de una función. En este caso, el denominador se anula en \(x=1\), consultando cómo resolver límites, se tiene
\(\lim\limits_{x\to 1^{-}}\frac{x(2x-1)}{x-1}=-\infty\)
\(\lim\limits_{x\to 1^{+}}\frac{x(2x-1)}{x-1}=\infty\)
Luego, hay una asíntota vertical en \(\bbox[yellow]{x=1}\)
. Asintótas horizontales:
Consultando cómo se resuelven límites, se tiene que
\(\lim\limits_{x\to\pm\infty}\frac{x(2x-1)}{x-1}=\frac{\pm\infty}{\pm\infty}\)
Se obtiene una indeterminación (ver indeterminaciones), para resolver el límite (ver cómo resolver límites), se utiliza la Regla de L’Hôpital (ver la Regla de L’Hôpital y la tabla de derivadas),
\(\lim\limits_{x\to\pm\infty}\frac{x(2x-1)}{x-1}=\lim\limits_{x\to\pm\infty}4x=\pm\infty\)
Luego, \(\bbox[yellow]{\hbox{no hay horizontales}}\)
. Asintótas oblicuas:
Las posibles asíntotas oblicuas tendrían la siguiente expresión \(y=mx+n\)
Con \(m=\lim\limits_{x\to\pm\infty}\frac{f(x)}{x}\), usando de nuevo
la Regla de L’Hôpital, se tiene
\(m=\lim\limits_{x\to\pm\infty}\frac{\frac{2x^2-x}{x-1}}{x}=\lim\limits_{x\to\pm\infty}\frac{2x^2-x}{x^2-x}=2\)
Y \(n=\lim\limits_{x\to\pm\infty}(f(x)-mx)=\lim\limits_{x\to\pm\infty}(\frac{2x^2-x}{x-1}-2x)=\lim\limits_{x\to\pm\infty}\frac{x}{x-1}=1\)
Luego, la recta \(\bbox[yellow]{y=2x+1}\) será asíntota oblicua
Los extremos relativos (máximos y mínimos) se estudiarán derivando la función e igualándola a cero, ver máximos y mínimos, la tabla de derivadas y consultar también cómo resolver polinomios
\(f'(x)=\frac{(4x-1)(x-1)-(2x^2-x).1}{(x-1)^2}=0\Rightarrow 2x^2-4x+1=0\Rightarrow x=1\pm\frac{\sqrt{2}}{2}\)
Para saber si los puntos críticos obtenidos son máximos o mínimos, se evalúan en la segunda derivada,
\(f»(x)=\frac{(4x-4)(x-1)-2(2x^2-4x+1)}{(x-1)^3}=\frac{2}{(x-1)^3}\)
Sustituyendo los valores obtenidos, \(x=1\pm\frac{\sqrt{2}}{2}\), se tiene que
\(f»(1-\frac{\sqrt{2}}{2})=\frac{2}{(1+\frac{\sqrt{2}}{2}-1)^3}=4\sqrt{2}>0\qquad\) y \(\qquad f»(1+\frac{\sqrt{2}}{2})=\frac{2}{(1-\frac{\sqrt{2}}{2}-1)^3}=-4\sqrt{2}<0\)
De esta forma, consultando cómo saber si los puntos críticos son máximos o mínimos, se concluye que (sabiendo que \(f(1\pm\frac{\sqrt{2}}{2})=3\pm2\sqrt{2}\)) la función tiene
\(\bbox[yellow]{\hbox{min. en }(1+\frac{\sqrt{2}}{2},3+2\sqrt{2})}\) y \(\bbox[yellow]{\hbox{max. en }(1-\frac{\sqrt{2}}{2},3-2\sqrt{2})}\)
b) Para representar la función se seguirán los pasos para dibujar el gráfico de una función
– El dominio en este caso serán todos los números reales menos el \(\{1\}\) ya que el denominador se anula en ese valor, ver dominio de una función
– Para calcular el corte con los ejes se iguala la función a cero, ver cómo obtener los cortes con los ejes
\(f(x)=0\Rightarrow 2x^2-x=0\Rightarrow x=0\) y \(x=\frac 12\), luego se tienen los puntos de corte \((0,0)\) y \((\frac 12,0)\)
Por otra parte, evaluando \(f(0)\) se tiene \(f(0)=0\), luego se obtiene el mismo punto de corte hallado antes, \((0,0)\)
Con estos datos y los obtenidos en el apartado anterior, es posible dibujar la función
c) Consultando la tabla de integrales y recordando cómo se resuelven integrales definidas y teniendo en cuenta algunas propiedades de los logaritmos, se tiene
\(\displaystyle\int_2^5\frac{f(x)}{x^2}dx=\displaystyle\int_2^5 \frac{\frac{x(2x-1)}{x-1}}{x^2}dx=\displaystyle\int_2^5 \frac{2x-1}{x^2-x}dx=\ln |x^2-x|\Big]_2^5=\ln 20-\ln 2=\ln\frac{20}{2}=\bbox[yellow]{\ln 10}\)
Ejercicio : (Septiembre 2012 Opción B) (Calificación: 3 ptos)
Dada la función: \(f(x)=\displaystyle\begin{cases}ax+b&x\leq 1\\ x^3-x^2+1&x>1\\\end{cases}\)
a) (1 pto) Calcúlense los valores de \(a\) y \(b\) para que la función sea continua y derivable
b) (1 pto) Para \(a=0\) y \(b=1\), hállase la ecuación de la recta tangente a la gráfica de \(f\) en los puntos en los que dicha tangente es paralela a la recta \(y-8x=1\)
c) (1 pto) Sea \(g\) la función real de variable real definida por \(g(x)=1-2x^2\). Para \(a=1\) y \(b=0\), calcúlese el área de la región plana acotada limitada por la gráfica de \(f\) y la gráfica de \(g\)
a) La función está formada por polinomios, luego el único punto de posible discontinuidad es el salto entre los polinomios, \(x=1\) (ver continuidad de funciones)
Para comprobar si la función es continua en dicho punto se evalúan los límites laterales y la función en el punto
\(\lim\limits_{x\to 1^{+}}f(x)=\lim\limits_{x\to 1^{+}}(x^3-x^2+1)=1\)
Calculando el otro límite lateral, se tiene
\(\lim\limits_{x\to 1^{-}}f(x)=\lim\limits_{x\to 1^{-}}(ax+b)=a.1+b=a+b=f(1)\)
Luego, para que la función sea continua en \(1\) (y, por tanto, en todo \(\mathbb{R}\)), se debe cumplir que \(a+b=1\)
Para que la función sea derivable tiene que cumplirse que \(f'(1^{-})=f'(1^{+})\), ver derivabilidad
En este caso, calculando primeramente la derivada de la función, se tiene
\(f'(x)=\displaystyle\begin{cases}a&x\leq 1\\ 3x^2-2x&x>1\\\end{cases}\)
Evaluando \(f'(1^{-})=f'(1^{+})\), se tiene que \(a=3.1^2-2.1\Rightarrow a=1\), luego, para que la función sea continua y derivable en todos los reales \(a+b=1,a=1\Rightarrow\bbox[yellow]{ a=1,b=0 }\)
b) Dos rectas paralelas tienen la misma pendiente y como la recta dada \(y=8x+1\) tiene pendiente \(8\), la ecuación de la recta tangente pedida también la tendrá, es decir, hay que buscar un punto en el cual la derivada de la función valga \(8\), ver ecuaciones de la recta
\(8=f'(x)=\displaystyle\begin{cases}1&x\leq 1\\ 3x^2-2x&x>1\\\end{cases}\Rightarrow 3x^2-2x=0\Rightarrow x=2\) y \(x=-\frac 43\)
El último valor, \(x=-\frac 43\), no está en el intervalo correspondiente al polinomio \(3x^2-2x\), por lo tanto, hay que quedarse sólamente con la solución \(x=2\)
La ecuación de la recta tangente en \(x=2\) viene dada por, ver ecuaciones de la recta
\(y-f(2)=f'(2)(x-2)\), con \(m\) la pendiente, en este caso es \(8\) y \(f(2)=2^3-2^2+1=5\)
Por lo tanto, se tendrá el resultado \(y-5=8(x-2)\Rightarrow\bbox[yellow]{y=8x-11}\)
c) Para hallar el área pedida primero hay que calcular los límites de integración, consultar cómo se calcula una integral definida
Dichos límites serán las soluciones del sistema de ecuaciones siguiente, ver cómo resolver sistemas de ecuaciones,
\(\displaystyle\begin{cases}\begin{cases}x&x\leq 1\\ x^3-x^2+1&x>1&\end{cases}\\g(x)=1-2x^2&\\\end{cases}\Rightarrow x=-1\) y \(x=\frac 12\)
Por lo tanto,
\(\displaystyle A=\int_{-1}^{\frac 12}(g(x)-f(x))dx=\int_{-1}^{\frac 12}(1-2x^2-x)dx=\int_{-1}^{\frac 12}(1-x-2x^2)dx=x-\frac{x^2}{2}-\frac{2x^3}{3}\Big]_{-1}^{\frac 12}=(\frac 12-\frac 18-\frac{1}{12})-(-1-\frac 12+\frac 23)=\bbox[yellow]{\frac 98}\)