Ejercicio :(Junio 2012 Opción A) (Calificación: 3 ptos)

Una empresa vinícola tiene plantadas \(1200\) cepas de vid en una finca, produciendo cada cepa una media de \(16\) Kg de uva. Existe un estudio previo que garantiza que por cada cepa que se añade a la finca, las cepas producen de media \(0,01\) Kg menos de uba cada una. Determínese el número de cepas que se deben añadir a las existentes para que la producción de uva de la finca sea máxima

Primeramente se determina la variable que se va a utilizar

\(x\equiv\) número de cepas que se deben añadir a la finca
\(P(x)\equiv\) producción (número de cepas por producción por cepa)

De esta forma, la ecuación a optimizar (maximizar en este caso) será

\(P(x)=(1200+x)(16-0,01x)\Rightarrow 19200+4x-0,01x^2\)

Para hallar le máximo pedido se deriva \(P(x)\) y se iguala a cero la derivada, ver cómo calcular máximos y mínimos de una función

\(P'(x)=4-0,02x=0\Rightarrow x=\frac{4}{0,02}=200\)

Para comprobar si es máximo o mínimo el punto crítico obtenido se evalúa en la segunda derivada,

\(P»(x)=-0,02<0\), luego, \(200\) es un máximo. Por lo tanto habrá que añadir \(\bbox[yellow]{200 \hbox{ cepas}}\)

Ejercicio : (Septiembre 2012 Opción A) (Calificación: 3 ptos)

Un pintor dispone de dos tipos de pintura para realizar su trabajo. El primer tipo de pintura tiene un rendimiento de \(3m^2\) por litro, con un coste de \(1\) euros por litro. El segundo tipo de pintura tiene un rendimiento de \(4m^2\) por litro, con un coste de \(1,2\) euros por litro. Con ambos tipos de pintura se puede pintar a un ritmo de \(1\) litro cada \(10\) minutos. El pintor dispone de un presupuesto de \(480\) euros y no puede pintar durante más de \(75\) horas. Además, debe utilizar al menos \(120\) litros de cada tipo de pintura. Determínese la cantidad de pintura que debe utilizar de cada tipo si su objetivo es pintar la máxima superficie posible. Indíquese cuál es la superficie máxima

Primeramente se identifican las variables del problema:

\(x\equiv\) Litros de pintura del primer tipo
\(y\equiv\) Litros de pintura del segundo tipo

La función a maximizar será \(F(x,y)=3x+4y\)

Las restricciones obtenidas a partir del enunciado serán las siguientes:

\(10x+10y\leq 75.60\Rightarrow x+y\leq 450\)

\(1x+1,2y\leq 480\Rightarrow 5x+6y\leq 2400\)

\(x\geq 120,\qquad y\geq 120\)

Para obtener los vértices de la región del enunciado, se resuelven las inecuaciones dos a dos, ver cómo resolver problemas de programación lineal y consultar cómo resolver sistemas de ecuaciones se obtiene el resultado

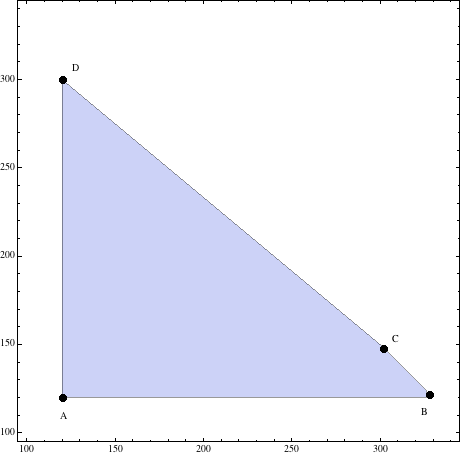
\(\displaystyle\begin{cases}x=&120\\y=&120\\\end{cases}\Rightarrow A(120,120)\)

\(\displaystyle\begin{cases}x+y=&450\\y=&120\\\end{cases}\Rightarrow B(330,120)\)

\(\displaystyle\begin{cases}x+y=&450\\5x+6y=&2400\\\end{cases}\Rightarrow C(300,150)\)

y

\(\displaystyle\begin{cases}x=&120\\5x+6y=&2400\\\end{cases}\Rightarrow D(120,300)\)

De forma que los vértices de la región pedida serán

\(\bbox[yellow]{A(120,120),\;B(300,150),\;C(120,300)\;y\;D(120,300)}\)

Y la región será

Sustituyendo los valores de los vértices de la región obtenida en la función objetivo \(F(x,y)=3x+4y\), se obtienen los siguientes resultados

\(\displaystyle\begin{cases}F(120,120)=&840\\F(330,120)=&1470\\F(300,150)=&1500\\F(120,300)=&1560\\\end{cases}\)

Luego, \(F(x,y)\) alcanza el valor máximo en el punto \(D(120,300)\)

Por lo tanto, serán necesarios \(\bbox[yellow]{120\hbox{ litros de pintura del primer tipo y }300\hbox{ litros del segundo tipo}}\)

Ver más ejercicios de Programación Lineal y Optimización en Selectividad