\[\]Ejercicio 1: Se considera el siguiente sistema de inecuaciones
\(\displaystyle\begin{cases}x+y\leq&3\\x-2y\leq&5 \\3x+y\geq&-1\\x\geq&0 \\\end{cases}\)
1. Dibujar el recinto cuyos puntos son las soluciones del sistema y obtener sus vértices
2. Hallar los puntos del recinto anterior en los que la función \(F(x,y)=x+3y\) toma los valores máximo y mínimo
1. Para obtener los vértices de la región pedida, se resuelven las ecuaciones dos a dos, ver cómo resolver problemas de programación lineal,
\(\displaystyle\begin{cases}x+y=&3\\x-2y=&5\\\end{cases}\Rightarrow (\frac{11}{3},-\frac{2}{3})\)
\(\displaystyle\begin{cases}3x+y=&-1\\x=&0\\\end{cases}\Rightarrow (0,-1)\)
\(\displaystyle\begin{cases}x-2y=&5\\3x+y=&-1\\\end{cases}\Rightarrow (\frac{3}{7},-\frac{16}{7})\)
y
\(\displaystyle\begin{cases}x+y=&3\\x=&0\\\end{cases}\Rightarrow (0,3)\)
De forma que los vértices de la región pedida serán \(\bbox[yellow]{A(0,3),\;B(\frac{11}{3},-\frac{2}{3}),\;C(\frac 37,-\frac{16}{7})\;y\;D(0,-1)}\)
Y la región será
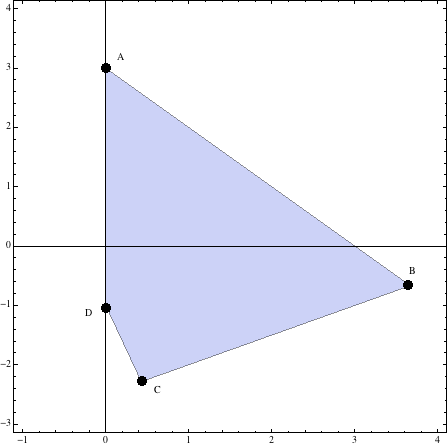
2. Sustituyendo los valores de los vértices de la región obtenida en la función objetiva \(F(x,y)\), se obtienen los siguientes resultados
\(\displaystyle\begin{cases}F(\frac{11}{3},-\frac{2}{3})=&\frac{11}{3}-2=\frac 53\\ F(0,-1)=&0-3=-3\\ F(\frac 37,-\frac{16}{7})=&-\frac{45}{7}\\ F(0,3)=&9\\\end{cases}\)
Luego, \(F(x,y)\) alcanza el valor máximo en el punto \(\bbox[yellow]{D(0,3)\;\hbox{y vale }9}\)
El valor mínimo se alcanza en \(\bbox[yellow]{C(\frac 37,-\frac{16}{7})\;\hbox{con valor }-\frac{45}{7}}\)
Ejercicio 2: Un fabricante de pizarras lanza una oferta especial en pizarras blancas y pizarras de tiza, ofreciendo las pizarras de tiza a un precio de \(200\) euros y las pizarras blancas un tercio más caras. La oferta está limitada: \(20\) pizarras de tiza y \(10\) blancas, además, el fabricante tiene el deseo de vender al menos tantas pizarras de tiza como pizarras blancas. Por otra parte, para cubrir gastos, los ingresos obtenidos deben ser, al menos, de \(2100\) euros
1. ¿Cuántas pizarras de cada modelo deberá vender para maximizar sus ingresos?
2. ¿Cuál será el importe de la venta?
Primeramente se identifican las variables a utilizar:
\(x:\;\hbox{pizarras de tiza vendidas}\)
\(y:\;\hbox{pizarras blancas vendidas}\)
Las restricciones dadas por el enunciado serán las siguientes
\(\displaystyle\begin{cases}0\leq x\leq 20&\\0\leq y\leq 10&\\x\geq y&\\200x+600y\geq 2100&\\\end{cases}\Rightarrow\begin{cases}0\leq x\leq 20&\\0\leq y\leq 10&\\x\geq y&\\x+3y\geq 10,5&\\\end{cases}\)
Resolviendo el sistema de inecuaciones, tomando dos a dos las ecuaciones, se obtendrán los vértices de la región buscada, ver cómo resolver problemas de programación lineal,
\(\displaystyle\begin{cases}x-20=&0\\y-10=&0\\\end{cases}\Rightarrow (20,10)\)
\(\displaystyle\begin{cases}x=&y\\x+3y=&10,5\\\end{cases}\Rightarrow (\frac{10,5}{4},\frac{10,5}{4})\)
\(\displaystyle\begin{cases}y-10=&0\\x=&y\\\end{cases}\Rightarrow (10,10)\)
\(\displaystyle\begin{cases}x-10=&0\\y=&0\\\end{cases}\Rightarrow (10,0)\)
y
\(\displaystyle\begin{cases}x-20=&0\\y=&0\\\end{cases}\Rightarrow (20,0)\)
De forma que los vértices de la región pedida serán
\(\bbox[yellow]{A(10,10),\;B(20,10),\;C(20,0),\;D(10,0)\;E(\frac{10,5}{4},\frac{10,5}{4})}\)
Y la región será
Sustituyendo los valores de los vértices \(A,\;B,\;C\;y\;D\) de la región obtenida en la función objetivo \(z(x,y)=200x+600y\), se obtiene
\(\displaystyle\begin{cases}z(20,10)=&4000+6000=10000\\z(\frac{10,5}{4},\frac{10,5}{4})=&2100\\z(10,10)=&2000+6000=8000\\z(10,0)=&2000\\z(20,0)=&4000\\\end{cases}\)
De forma que el máximo de la función \(z(x,y)\) se alcanza en el punto \(C(20,10)\), es decir,
\(\bbox[yellow]{\hbox{el fabricante tiene que vender }10\hbox{ pizarras blancas y }20\hbox{ pizarras de tiza}}\)
2. El ingreso máximo será de \(\bbox[yellow]{z(20,10)=10000\hbox{ euros}}\)
\[\] Ejercicio 3: Un montador de abanicos dispone de dos modelos \(A\) y \(B\). El modelo \(A\) requiere para su fabricación, \(20\;\hbox{cm}^2\) de papel, \(120\;\hbox{cm}^2\) de lámina de madera y \(1\) enganche metálico. El modelo \(B\) requiere \(60\;\hbox{cm}^2\) de papel, \(80\;\hbox{cm}^2\) de lámina de madera y \(1\) enganche metálico. El coste de producción de cada modelo es de \(1,20\;\hbox{euros}\) el modelo \(A\) y \(1,30\;\hbox{euros}\) el \(B\). El precio de vente es de \(1,80\;\hbox{euros}\) cada uno, independientemente del modelo. Teniendo en cuenta que las existencias son de \(3000\;\hbox{cm}^2\) de papel, \(7200\;\hbox{cm}^2\) de lámina y \(70\) enganches
1. Representar la región factible
2. Determinar el número de abanicos de cada modelo que ha de hacer para obtener un beneficio máximo
3. Calcular dicho beneficio
Nombrando en primer lugar las variables a utilizar, se tiene:
\(x:\;\hbox{abanicos del modelo }A\)
\(y:\;\hbox{abanicos del modelo }B\)
Las restricciones dadas por el enunciado son
\(\displaystyle\begin{cases}20x+60y\leq&3000\\120x+80y\leq&7200\\x+y\leq &70\\x,\;y\geq&0\\\end{cases}\Rightarrow\begin{cases}x+3y\leq&150\\3x+2y\leq&180\\x+y\leq &70\\x,\;y\geq&0\\\end{cases}\)
Resolviendo dos a dos el sistema de inecuaciones, se obtienen los vértices de la región buscada, ver cómo resolver problemas de programación lineal,
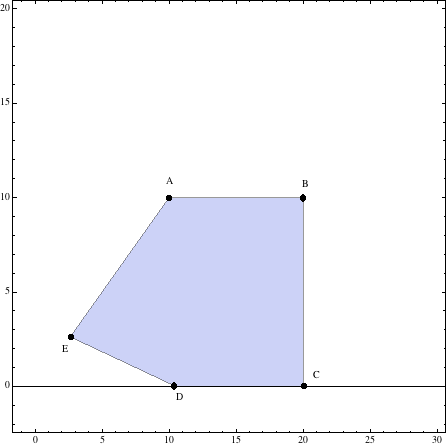
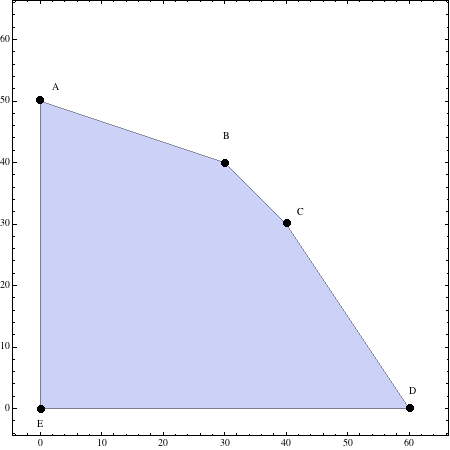
\(\bbox[yellow]{A(0,50),\;B(30,40),\;C(40,30),\;D(60,0)\;y\;E(0,0)}\)
Para dibujar la región se tendrán en cuenta estos vértices así como la restricción \(x,\;y\geq 0\),
2. El beneficio viene dado por la función \(z(x,y)=0,60x+0,50y\). Sustituyendo los valores de los vértices \(A,\;B,\;C\;y\;D\) en la función \(z(x,y)\), se obtiene
\(\displaystyle\begin{cases}z(60,0)=&36\\z(40,30)=&39\\z(30,40)=&38\\z(0,50)=&25\\\end{cases}\)
El máximo beneficio se obtiene fabricando \(\bbox[yellow]{ 40\hbox{ abanicos del modelo }A\hbox{ y }30\hbox{ abanicos del }B}\)
3. El beneficio máximo será de \(\bbox[yellow]{39\hbox{ euros}}\)
\[\]Ejercicio 4: Sea \(S\) la región del plano de coordenadas mayores o iguales que cero y tales que sus puntos cumplen que
– La media aritmética de las coordenadas es menor o igual que \(3\)
– El doble de la abcisa más la ordenada es mayor o igual que \(3\)
1. Representar gráficamente el conjunto \(S\)
2. Determinar en qué puntos de \(S\) la función \(f(x,y)=x-2y\) toma el valor máximo
1. Las restricciones del recinto serán
\(\displaystyle\begin{cases}\frac{x+y}{2}\leq&5\\2x+y\geq&5\\x,\;y\geq&0\\\end{cases}\Rightarrow\begin{cases}x+y\leq&10\\2x+y\geq&5\\x,\;y\geq&0\\\end{cases}\)
Tomando dos a dos el sistema de inecuaciones, se obtienen los vértices de la región buscada, ver cómo resolver problemas de programación lineal,
\(\displaystyle\begin{cases}x+y=&10\\x=&0\\\end{cases}\Rightarrow (0,10)\)
\(\displaystyle\begin{cases}x+y=&10\\y=&0\\\end{cases}\Rightarrow (10,0)\)
\(\displaystyle\begin{cases}2x+y=&5\\x=&0\\\end{cases}\Rightarrow (0,5)\)
y
\(\displaystyle\begin{cases}2x+y=&5\\y=&0\\\end{cases}\Rightarrow (\frac 52,0)\)
De forma que los vértices de la región pedida serán
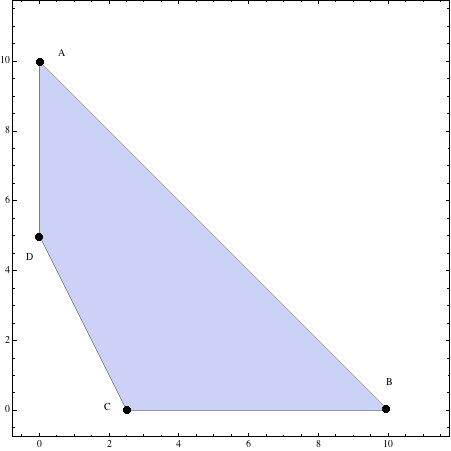
\(\bbox[yellow]{A(0,10),\;B(10,0),\;C(\frac 52,0)\;y\;D(0,5)}\)
Para dibujar la región se tendrán en cuenta estos vértices,
2. Evaluando la función \(f(x,y)\) en los vértices de la región \(S\), ver programación lineal, se tiene
\(\displaystyle\begin{cases}f(\frac 52,0)=&\frac 52\\f(0,5)=&-\frac 52\\f(10,0)=&10\\f(0,10)=&-10\\\end{cases}\)
El valor máximo es \(\bbox[yellow]{ 10\hbox{ y corresponde al punto }(10,0)}\)
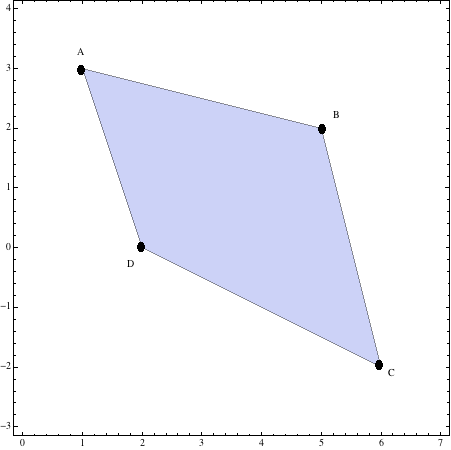
\[\]Ejercicio 5: El cuadrilátero \(ABCD\) es la región solución de un sistema de inecuaciones lineales con \(A(1,3),\;B(5,2),\;C(6,-2),\;y\;D(2,0)\)
1. Encontrar los valores máximo y mínimo de la función \(f(x,y)=2x+y\) en dicha región
2. ¿En qué puntos de la región solución la función del apartado anterior alcanza el máximo y el mínimo?
1. Primeramente se dibuja el cuadrilátero con los datos dados \(A,\;B,\;C,\;y\;D\)
2. Evaluando la función \(f(x,y)\) dada en los vértices, ver programación lineal, se tiene
\(\displaystyle\begin{cases}f(1,3)=&5\\f(6,-2)=&10\\f(2,0)=&4\\f(5,2)=&12\\\end{cases}\)
El valor máximo es \(\bbox[yellow]{ 12\hbox{ y corresponde al punto }(5,2)}\)
El valor mínimo es \(\bbox[yellow]{ 4\hbox{ y corresponde al punto }(2,0)}\)