Ejercicio : (Junio 2010 Opción A) (Calificación: 3 ptos)
Se considera la función \(f(x)=-0,4x+3,2y\) sujeta a las siguientes restricciones
\(\displaystyle\begin{cases}x+y\leq&7\\x+4y\geq&4\\x+5\geq&4\\0\leq x\leq 5&\\y\geq 0,&\\\end{cases}\)
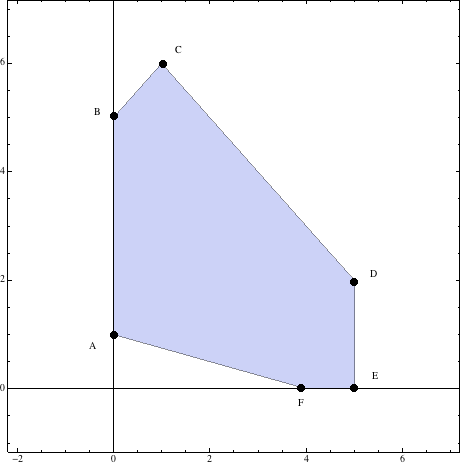
a) Represéntese la región \(S\) del plano determinada por el conjunto de restricciones
b) Calcúlense los puntos de la región \(S\) donde la función \(f\) alcanza sus valores máximo y mínimo
c) Calcúlense dichos valores máximo y mínimo
a) Para obtener los vértices de la región pedida, se resuelven las ecuaciones dos a dos, ver cómo resolver problemas de programación lineal y consultar cómo resolver sistemas de ecuaciones se obtiene el resultado
\(\displaystyle\begin{cases}x=&0\\x+4y=&4\\\end{cases}\Rightarrow A(0,1)\)
\(\displaystyle\begin{cases}x=&0\\x-y=&-5\\\end{cases}\Rightarrow B(0,5)\)
\(\displaystyle\begin{cases}x+y=&7\\x-y=&-5\\\end{cases}\Rightarrow C(1,6)\)
\(\displaystyle\begin{cases}x+y=&7\\x=&5\\\end{cases}\Rightarrow D(5,2)\)
y
\(\displaystyle\begin{cases}y=&0\\x=&5\\\end{cases}\Rightarrow E(5,0)\)
De forma que la región pedida será
b) Sustituyendo los valores de los vértices de la región obtenida en la función objetiva \(f(x,y)\), se obtienen los siguientes resultados
\(\displaystyle\begin{cases}f(0,1)=&3,2\\f(0,5)=&16\\f(1,6)=&18,8\\f(5,2)=&4,4\\f(5,0)=&-2\\f(4,0)=&-1,6\\\end{cases}\)
Luego, \(f(x,y)\) alcanza el valor mínimo en el punto \(\bbox[yellow]{E(5,0)}\) y el máximo en \(\bbox[yellow]{C(1,6)}\)
c) Los valores serán \(\bbox[yellow]{f(1,6)=18,8}\) y \(\bbox[yellow]{f(5,0)=-2}\)
Ejercicio :(Junio 2010 Opción A) (Calificación: 3 ptos)
Se considera el rectángulo \(R\) de vértices \(BOAC\) con \(B(0,b)\), \(O(0,0)\), \(A(a,0)\) y \(C(a,b)\) con \(a>0,b>0\) y cuyo vértices \(C\) está situado en la parábola de ecuación \(y=-x^2+12\)
a) (1 pto) Para \(a=3\), determínense las coordenadas de los vértices de \(R\) y calcúlese el área de \(R\)
b) (1 pto) Determínense las coordenadas de los vértices de \(R\) de manera que el área del rectángulo sea máxima
c) (1 pto) Calcúlese el valor de dicha área máxima
a) Si \(a=3\) y el vértice de la parábola viene dado por \(C(a,b)\), se tendrá que \(b=-3^2+12=3\), ver geometría de una parábola
De manera que y se tienen los vértices dle rectángulo \(R\) buscado, \(O(0,0),\; A(3,0),\; C(3,3),\; D(0,3)\)
El área del un rectángulo viene determinada por \(A=a.b\), ver área de un rectángulo
Por lo tanto, \(A=3.3=\bbox[yellow]{9}\)
b) Sabiendo que el punto \(C\) pertenece a la parábola y, por otra parte, teniendo en cuenta la fórmula del área del rectángulo, los parámetros \(a,b\) tienen que cumplir que
\(\begin{cases}b=-a^2+12&\\A=a.b&\\\end{cases}\Rightarrow A=-a^3+12a\)
Para hallar el máximo pedido se deriva la función \(A(a)\) y se iguala a cero la derivada, ver cómo calcular máximos y mínimos de una función y consultar también la tabla de derivadas,
\(A'(a)=-3a^2+12=0\Rightarrow a=\pm 2\)
El valor negativo de \(a\) no tiene sentido (ya que se está hablando de la medida de un lado de un rectángulo), luego sólo se tendrá en cuenta \(a=2\)
Para comprobar si es máximo el punto crítico obtenido se evalúa en la segunda derivada,
\(A»(a)=-6a\) y \(A»(2)=-12<0\), luego, en \(a=2\quad\hbox{y }b=-2^2+12=8\) se alcanza un máximo para el área del rectángulo
Por lo tanto, el rectángulo de área máxima tendrá los siguientes vértices
\(\bbox[yellow]{O(0,0),\; A(2,0),\; C(2,8),\; D(0,8)}\)
c) Sustituyendo los valores hallados en el apartado anterior (\(a=2,b=8\)), se tiene \(A=2.8\Rightarrow\bbox[yellow]{A=16}\)
Ver más ejercicios de Programación Lineal y Optimización en Selectividad