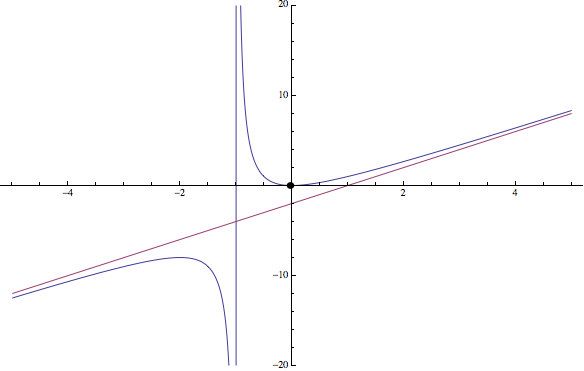
\[\]Ejercicio 5: Representar la función \(f(x)=\frac{2x^2}{x+1}\)
Para representar la función se seguirán los pasos para dibujar el gráfico de una función
– Se trata de una función racional, luego el dominio de la función será todos los números reales excepto los puntos que hacen el denominador (\(x+1\)) cero, ver cómo calcular el dominio de una función
Luego, el dominio son todos los reales menos el \(-1\)
– Para calcular el corte con los ejes se iguala la función a cero, ver cómo obtener los cortes con los ejes
\(f(x)=0\Rightarrow x=0\), luego la función pasará por el origen de corrdenadas, \((0,0)\)
Por otra parte, como \(f(0)=0\), se obtiene el mismo punto de corte, \((0,0)\)
– Para estudiar las asintótas de la función, consultar el apartado de teoría de asíntotas
. Asintótas verticales:
\(\lim\limits{x\to -1}\frac{2x^2}{x+1}=\frac 20=\infty\)
Luego, \(x=-1\) es una asíntota vertical
. Asintótas horizontales:
\(\lim\limits{x\to\infty}\frac{2x^2}{x+1}=\infty\)
Luego, no hay asíntotas horizontales
. Asintótas oblicuas:
Las asíntotas oblicuas serían de la forma \(y=mx+n\), con
\(m=\lim\limits{x\to\infty}\frac{f(x)}{x}=\lim\limits{x\to\infty}\frac{2x^2}{x^2+x}\)
Utilizando la Regla de L’Hôpital se obtiene que \(m=2\)
Por otra parte,
\(n=\lim\limits{x\to\infty}(f(x)-2x)=\lim\limits{x\to\infty}\frac{-2x}{x+1}=-2\)
Luego, \(y=2x-2\) es una asíntota oblicua
– Los intervalos de crecimiento y decrecimiento se estudiarán calculando los máximos y mínimos de la función, ver máximos y mínimos y la tabla de derivadas
\(f'(x)=\frac{4x(x+1)-2x^2}{(x+1)^2}=0\Rightarrow x(2x+4)=0\Rightarrow x=0\) y \(x=-2\)
Para saber si los puntos críticos obtenidos son máximos o mínimos se evalúan en la segunda derivada,
\(f»(x)=\frac{(4x+4)(x+1)^2-2(x+1)(2x^2+4x)}{(x+1)^4}\)
De esta forma se concluye que la función tiene un máximo en \((-2,-8)\) y un mínimo en \((0,0)\)
– Para estudiar la curvatura de la función se hallan los puntos de inflexión de \(f(x)\), ver cómo estudiar la curvatura de una función
\(f»(x)=\frac{(4x+4)(x+1)^2-2(x+1)(2x^2+4x)}{(x+1)^4}\Rightarrow\frac{4}{(x+1)^3}=0\)
No hay puntos de inflexión ya que la segunda derivada no se puede anular
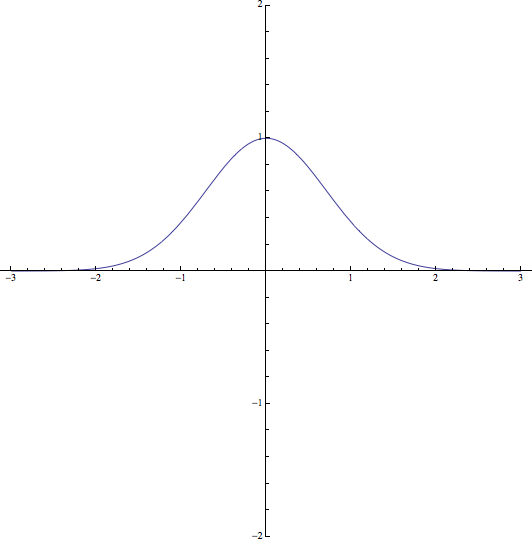
\[\] Ejercicio 6: Representar la función \(f(x)=\frac{1}{e^{x^2}}\)
Para representar la función se seguirán los pasos para dibujar el gráfico de una función
– El dominio de la función serán todos los números reales, ver cómo calcular el dominio de una función
– Para calcular el corte con los ejes se iguala la función a cero y se iguala también \(x\) a cero, ver cómo obtener los cortes con los ejes y ver cómo se resuelven polinomios,
\(f(x)=0\Rightarrow\hbox{Imposible}\), luego la función no corta al eje \(OX\)
Por otra parte, \(f(0)=1\), luego la función pasará por el punto \((0,1)\)
– Como el dominio de la función son todos los números reales, la función no tendrá asíntotas verticales, ver asíntotas
. Asintótas horizontales:
\(\lim\limits{x\to\infty}\frac{1}{e^{x^2}}=0\)
Luego, la recta \(y=0\) es una asíntota horizontal de la función
. Asintótas oblicuas: No hay ya que hay horizontales
– Los intervalos de crecimiento y decrecimiento se estudian calculando los máximos y mínimos de \(f(x)\), ver máximos y mínimos y la tabla de derivadas
\(f'(x)=-2xe^{-x^2}=0\Rightarrow x=0\)
Para comprobar si el punto obtenido es máximo o mínimo se estudia el signo de la segunda derivada en el punto crítico
\(f»(x)=-2e^{-x^2}+(-2xe^{-x^2})(-2x)=\frac{4x-2}{e^{x^2}}\)
y \(f»(0)=-2<0\), de forma que \((0,1)\) es un máximo de la función
– Para estudiar la curvatura de la función se hallan los puntos de inflexión de \(f(x)\), ver cómo estudiar la curvatura de una función
\(f»(x)=\frac{4x-2}{e^{x^2}}=0\Rightarrow x=\frac 12\), luego el punto de inflexión se encontrará en \((\frac 12,f(\frac 12))\)
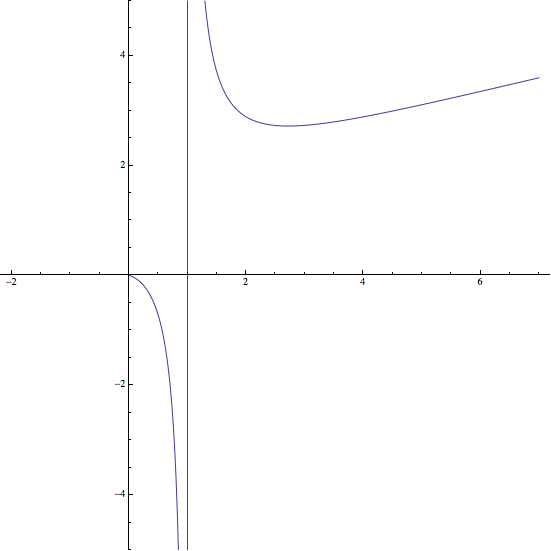
\[\] Ejercicio 7: Representar la función \(f(x)=\frac{x}{\ln x}\)
Para representar la función se seguirán los pasos para dibujar el gráfico de una función
– El dominio de la función serán todos los números reales positivos, \((0,\infty)\), porque es el rango para el cual la función logaritmo tiene sentido, menos los puntos que hacen el denominador igual a cero (\(x=1\)), ver cómo calcular el dominio de una función
– Para calcular el corte con los ejes se iguala la función a cero y se iguala también \(x\) a cero, ver cómo obtener los cortes con los ejes
\(f(x)=0\Rightarrow x=0\), como \(x=0\) no está en el dominio, no hay puntos de corte con los ejes
– Para estudiar la existencia de asíntotas, ver la teoría de asíntotas
. Asintótas verticales:
\(\lim\limits{x\to 1}\frac{x}{\ln x}=\infty\)
Luego, la recta \(x=1\) es una asíntota vertical de la función
. Asintótas horizontales : No hay
. Asintótas oblicuas: No hay
– Los intervalos de crecimiento y decrecimiento se estudian calculando los máximos y mínimos de \(f(x)\), ver máximos y mínimos y la tabla de derivadas
\(f'(x)=\frac{\ln x -1}{(\ln x)^2}=0\Rightarrow \ln x=1\Rightarrow x=e\)
Para comprobar si el punto obtenido es máximo o mínimo se estudia el signo de la segunda derivada en el punto
\(f»(x)=\frac{\frac 1x(\ln x)^2-(\ln x -1)\frac 2x \ln x}{(\ln x)^4}\) y \(f»(e)>0\)
Luego \((e,e)\) es un mínimo de la función
Con los puntos estudiados se tiene suficiente información para hacer el gráfico pedido
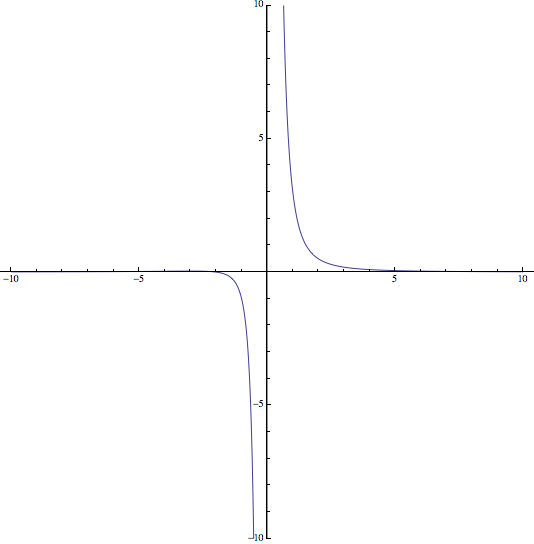
\[\] Ejercicio 8: Representar la función \(f(x)=\frac{x+2}{x^3}\)
Para representar la función se seguirán los pasos para dibujar el gráfico de una función
– Como la función es racional, el dominio será todos los números reales menos los que hacen el denominador cero, es decir, todos los reales menos el cero, ver cómo calcular el dominio de una función
– Para calcular el corte con los ejes se iguala la función a cero y se iguala también \(x\) a cero, ver cómo obtener los cortes con los ejes
\(f(x)=0\Rightarrow x=-2\), luego la función pasará por el punto \((-2,0)\)
Por otra parte, \(f(0)=\infty\), por lo que la función no corta al eje \(OY\)
– Para el siguiente apartado ver la parte de teoría sobre asíntotas
. Asintótas verticales:
\(\lim\limits{x\to 0}\frac{x+2}{x^3}=\infty\)
Luego, la recta \(x=0\) es una asíntota vertical de la función
. Asintótas horizontales:
\(\lim\limits{x\to\pm\infty}\frac{x+2}{x^3}=\frac{\infty}{\infty}\)
Utilizando la Regla de L’Hôpital, se obtiene
\(\lim\limits{x\to\pm\infty}\frac{x+2}{x^3}=0\)
Luego, \(y=0\) será una asíntota horizontal
. Asintótas oblicuas: No hay ya que hay horizontales
– Los intervalos de crecimiento y decrecimiento se estudian calculando los máximos y mínimos de \(f(x)\), ver máximos y mínimos y la tabla de derivadas
\(f'(x)=\frac{-2x^3-6x^2}{x^6}=0\Rightarrow x=0\) y \(x=-3\)
Para comprobar si el punto obtenido es máximo o mínimo se estudia el signo de la segunda derivada en el punto crítico
\(f»(x)=\frac{6x^8+24x^7}{x^{12}}\)
y \(f»(-3)<0\), de forma que \((-3,\frac{1}{27})\) es un máximo de la función
Los datos obtenidos son suficientes para dibujar la función
Ver ejercicios de repaso de Representación de funciones