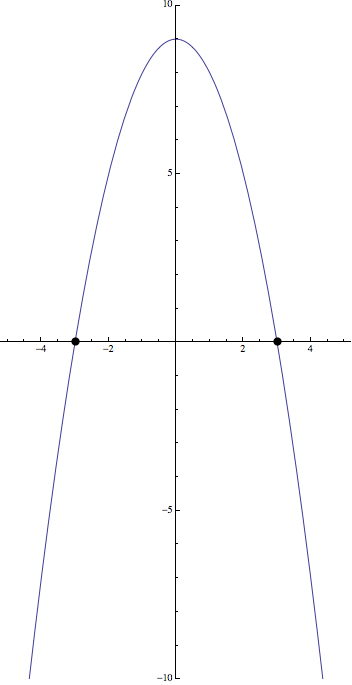
\[\]Ejercicio 1: Representar la función \(f(x)=9-x^2\)
Se trata de una parábola, ver representación de funciones elementales
En este caso es una parábola hacia abajo, con el vértice en \((0,9)\)
Para poder dibujarla es importante saber dónde corta con el eje \(X\), ver cómo obtener los cortes con los ejes
Es decir, \(f(x)=0\Rightarrow x=\pm 3\Rightarrow f(x)\) corta al eje \(X\) en \((-3,0)\) y en \((3,0)\)
Luego, el dibujo quedaría
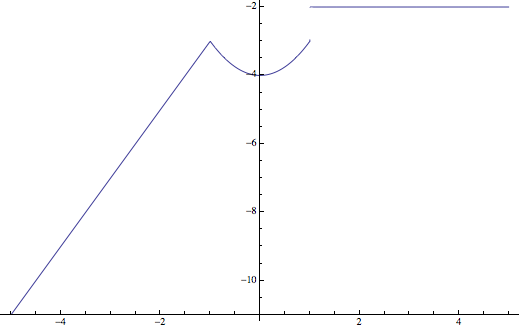
Ejercicio 2: Representar la función \(f(x)=\begin{cases}2x-1&\hbox{si }x<-1\\x^2-4&\hbox{si }-1\leq x<1\\-2&\hbox{si }x\geq 1\\\end{cases}\)
Se trata de una función a trozos formada por una recta, \(2x-1\), ver ecuaciones de la recta, una parábola, \(x^2-4\), ver representación de funciones elementales y una constante, \(-2\)
Para dibujar la recta, se dan dos valores a la \(x\) y se obtienen dos puntos de dicha recta y se unen
La parábola \(x^2-4\) es una parábola hacia arriba con vértice en \((0,-4)\)
De esta forma, el dibujo quedaría
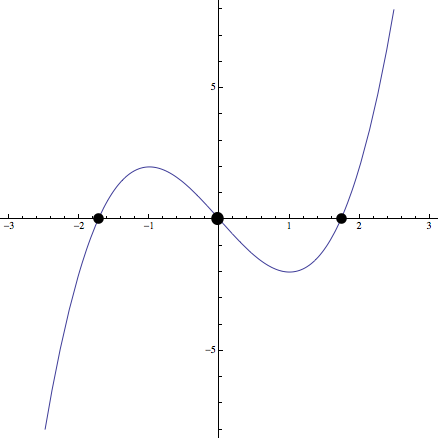
\[\] Ejercicio 3: Representar la función \(f(x)=x^3-3x\)
Se trata de una función polinómica, ver representación de funciones elementales
– El dominio de dicha función es todo los números reales, ver cómo calcular el dominio de una función
– Para calcular el corte con los ejes se iguala la función a cero y se iguala también \(x\) a cero, ver cómo obtener los cortes con los ejes
\(f(x)=0\Rightarrow x=-1,\;x=\frac 12\) y \(f(0)=0\), luego los cortes con los ejes serán \((-1,0)\), \((\frac 12, 0)\) y \((0,0)\)
– Las funciones polinómicas no tienen asíntotas, ver asíntotas
Para ver su comportamiento en el infinito, ver cómo resolver límites, se estudian
\(\lim\limits_{x\to\infty}x^3-3x=\infty\) y \(\lim\limits_{x\to -\infty}x^3-3x=-\infty\)
– Los intervalos de crecimiento y decrecimiento se estudiarán calculando los máximos y mínimos de la función, ver máximos y mínimos y la tabla de derivadas
\(f'(x)=3x^2-3=0\Rightarrow x=\pm 1\)
Para comprobar si los puntos obtenidos son máximos o mínimos se estudia la segunda derivada de \(f(x)\): \(f»(x)=6x\)
Luego, \(f»(-1)<0\) y \((-1, f(-1)=2)\) es un máximo y \(f»(1)>0\) por lo que \((1,f(1)=-2)\) es un mínimo
– Para estudiar la curvatura de la función se hallan los puntos de inflexión de \(f(x)\), ver cómo estudiar la curvatura de una función
\(f»(x)=6x=0\Rightarrow x=0\)
Luego, \(x=0\) es un punto de inflexión (de cambio de curvatura), para ver cómo varía la función se estudia el signo de la segunda derivada antes y después de \(x=0\)
En este caso \(f»(x<0)<0\) y \(f»(x>0)>0\), luego antes del cero la función será convexa y a partir de dicho punto, cóncava
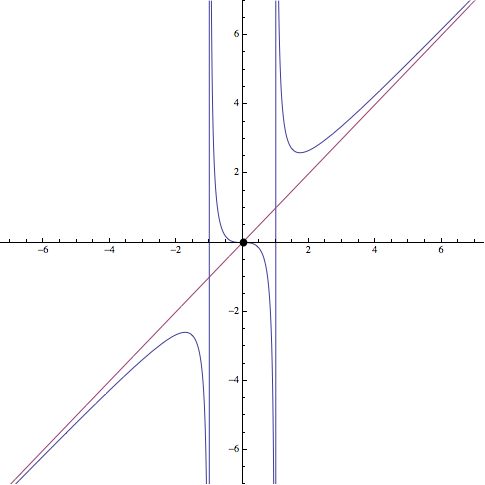
\[\]Ejercicio 4: Representar la función \(f(x)=\frac{x^3}{x^2-1}\)
Se trata de una función racional, ver representación de funciones elementales
– El dominio de dicha función serán todos los números reales excepto los que hacen que el denominador se anule, ver cómo calcular el dominio de una función
\(x^2-1=0\Rightarrow x=\pm 1\)
Luego, el dominio serán todos los números reales menos \(\pm 1\)
– Para calcular el corte con los ejes se iguala la función a cero y se iguala también \(x\) a cero, ver cómo obtener los cortes con los ejes
\(f(x)=0\Rightarrow x^3=0\Rightarrow x=0,\) y \(f(0)=0\), luego los cortes con los ejes serán \((0,0)\)
– Para estudiar las asíntotas de la función consultar asíntotas y ver cómo resolver límites
. Asíntotas verticales:
\(\lim\limits_{x\to -1^{-}}\frac{x^3}{x^2-1}=-\infty\) y \(\lim\limits_{x\to -1^{+}}\frac{x^3}{x^2-1}=\infty\), luego en \(x=-1\) hay una asíntota vertical
\(\lim\limits_{x\to 1^{-}}\frac{x^3}{x^2-1}=-\infty\) y \(\lim\limits_{x\to 1^{+}}\frac{x^3}{x^2-1}=\infty\), luego en \(x=1\) hay una asíntota vertical
. Asíntotas horizontales: No hay (ver asíntotas)
. Asíntotas oblicuas: La asíntota será de la forma \(y=mx+n\), con
\(m=\lim\limits_{x\to\infty}\frac{f(x)}{x}=\lim\limits_{x\to\infty}\frac{x^3}{x(x^2-1)}\)
Recordando la Regla de L’Hôpital se tiene que \(m=1\)
Por otra parte,
\(n=\lim\limits_{x\to\infty}(f(x)-mx)=\lim\limits_{x\to\infty}\frac{x^3-x^3+x}{x^2-1}\)
Aplicando de nuevo la Regla de L’Hôpital, \(n=0\)
Luego, la asíntota oblicua será la recta \(y=x\)
– Los intervalos de crecimiento y decrecimiento se estudian calculando los máximos y mínimos de \(f(x)\), ver máximos y mínimos y la tabla de derivadas
\(f'(x)=\frac{x^4-3x^2}{(x^2-1)^2}=0\Rightarrow x=\pm \sqrt{3}\) y \(x=0\)
Para comprobar si los puntos obtenidos son máximos o mínimos se estudia la segunda derivada de \(f(x)\): \(f»(x)=\frac{2x(x^2+3)}{(x^2-1)^3}\)
Luego, \(f»(0)=0\) y \((0, f(0)=0)\) hay un punto de inflexión
Por otra parte \(f»(\sqrt{3})>0\) por lo que \((\sqrt{3},f(\sqrt{3}))\) es un mínimo y \(f»(-\sqrt{3})<0\) por lo que \((-\sqrt{3},f(-\sqrt{3}))\) es un máximo
– Para estudiar la curvatura de la función se hallan los puntos de inflexión de \(f(x)\), ver cómo estudiar la curvatura de una función
\(f»(x)=0\Rightarrow x=0\)
Luego, \(x=0\) es un punto de inflexión (de cambio de curvatura), para ver cómo varía la función se estudia el signo de la segunda derivada antes y después de \(x=0\)
En este caso \(f»(x<0)<0\) y \(f»(x>0)>0\), luego antes del cero la función será convexa y a partir de dicho punto, cóncava
Ver ejercicios más avanzados de Representación de funciones