\[\]Ejercicio 4: Estudiar las asíntotas verticales de la función \(f(x)=\sec x\)
La función puede escribirse como \(\sec x=\frac{1}{\cos x}\), ver ecuaciones trigonométricas
De forma que las posibles asíntotas verticales de la función serán las soluciones de \(\cos x=0\). Es decir, \(x=\frac{\pi}{2}+k\pi\), \(k\in\mathbb{Z}\), ver asíntotas
Como \(f(x)=\sec x\) es una función periódica (de período \(2\pi\)), bastará estudiarla en \(\frac{\pi}{2}\) y \(-\frac{\pi}{2}\), ver cómo resolver límites
\(\lim\limits_{x\to \frac{\pi}{2}^{+}}\frac{1}{\cos x}=-\infty\) y \(\lim\limits_{x\to \frac{\pi}{2}^{-}}\frac{1}{\cos x}=\infty\), luego en \(\bbox[yellow]{x=\frac{\pi}{2}}\) hay una asíntota vertical
\(\lim\limits_{x\to -\frac{\pi}{2}^{+}}\frac{1}{x^2-2x}=\infty\) y \(\lim\limits_{x\to -\frac{\pi}{2}^{-}}\frac{1}{\cos x}=-\infty\), luego en \(\bbox[yellow]{x=-\frac{\pi}{2}}\) hay otra asíntota vertical
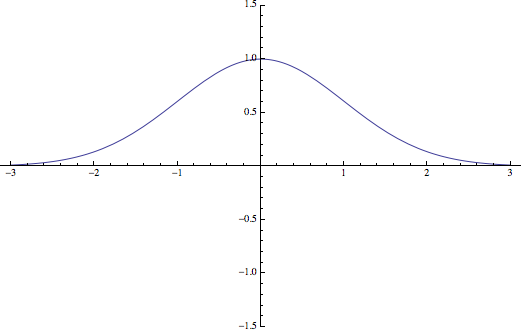
\[\]Ejercicio 5: Representar la función \(f(x)=e^{-\frac{x^2}{2}}\)
Para representar la función se seguirán los pasos para dibujar el gráfico de una función
– El dominio de la función serán todos los números reales, ver cómo calcular el dominio de una función
– Para calcular el corte con los ejes se iguala la función a cero y se iguala también \(x\) a cero, ver cómo obtener los cortes con los ejes
\(f(x)=0\Rightarrow e^{-\frac{x^2}{2}}=0\Rightarrow\hbox{Imposible}\) y \(f(0)=1\), luego los cortes con los ejes serán \((0,1)\)
– Para estudiar las asíntotas de la función consultar asíntotas y ver cómo resolver límites
. Asíntotas verticales: No hay ya que no hay puntos fuera del dominio de \(f(x)\)
. Asíntotas horizontales:
\(\lim\limits_{x\to\pm\infty}e^{-\frac{x^2}{2}}=0\), luego la recta \(y=0\) es una asíntota vertical de la función
. Asíntotas oblicuas: No hay ya que hay asíntotas horizontales, ver asíntotas
– Los intervalos de crecimiento y decrecimiento se estudian calculando los máximos y mínimos de \(f(x)\), ver máximos y mínimos y la tabla de derivadas
\(f'(x)=e^{-\frac{x^2}{2}}\big(-\frac{2x}{2}\big)=-xe^{-\frac{x^2}{2}}=0\Rightarrow x=0\)
Para comprobar si el punto obtenido es máximo o mínimo se estudia el signo de la primera derivada antes y después de dicho punto \(f'(x<0)<0\) y \(f'(x>0)>0\), luego \((0,1)\) es un máximo
– Para estudiar la curvatura de la función se hallan los puntos de inflexión de \(f(x)\), ver cómo estudiar la curvatura de una función
\(f»(x)=-e^{-\frac{x^2}{2}}-xe^{-\frac{x^2}{2}}\big(-\frac{2x}{2}\big)=e^{-\frac{x^2}{2}}(x^2-1)=0\Rightarrow x=\pm 1\)
Luego, \((-1,e^{-\frac{1}{2}})\) y \((1,e^{-\frac{1}{2}})\) son puntos de inflexión (de cambio de curvatura), para ver cómo varía la función se estudia el signo de la segunda derivada antes y después de ambos puntos
En este caso la función será cóncava en \((-\infty, -1)\) y \((1,\infty)\) y es convexa en \((-1,1)\)
Ver ejercicios de repaso de representación de funciones
Ver ejercicios más avanzados de Representación de funciones