OPCIÓN B
\[\]Ejercicio 1: (3 ptos) Un pintor necesita pintura para pintar como mínimo una superficie de \(480m^2\). Puede comprar la pintura a dos proveedores, \(A\) y \(B\). El proveedor \(A\) le ofrece una pintura con un rendimiento de \(6m^2\) por Kg y un precio de \(1\) euro por Kg. La pintura del proveedor \(B\) tiene un precio de \(1,2\) euros por Kg y un rendimiento de \(8m^2\) por Kg. Ningún proveedor le puede suministrar más de \(75\) Kg de pintura y el presupuesto máximo del pintor es de \(120\) euros. Calcúlese la cantidad de pintura que el pintor tiene que comprar a cada proveedor para obtener el mínimo coste. Calcúlese dicho coste mínimo
Primeramente se identifican las variables del problema:
\(x\equiv\) Kg de pintura comprados al proveedor \(A\)
\(y\equiv\) Kg de pintura comprados al proveedor \(B\)
La función a maximizar será \(F(x,y)=1x+1,2y\)
Las restricciones obtenidas a partir del enunciado serán las siguientes:
\(6x+8y\geq 480,\quad\)\(\quad 0\leq x\leq 75,\quad\)\(\quad 0\leq y\leq 75,\quad\)\(\quad x+1,2y\leq 120,\quad\)\(\quad x\geq 0,\qquad y\geq 0\)
Para obtener los vértices de la región del enunciado, se resuelven las inecuaciones dos a dos, ver cómo resolver problemas de programación lineal y consultar cómo resolver sistemas de ecuaciones se obtiene el resultado
\(\displaystyle\begin{cases}x=&0\\6x+8y=&480\\\end{cases}\Rightarrow A(0,60)\)
\(\displaystyle\begin{cases}x=&0\\y=&75\\\end{cases}\Rightarrow B(0,75)\)
\(\displaystyle\begin{cases}x+1,2y=&120\\y=&75\\\end{cases}\Rightarrow C(30,75)\)
\(\displaystyle\begin{cases}x+1,2y=&120\\x=&75\\\end{cases}\Rightarrow D(75,37.5)\)
y
\(\displaystyle\begin{cases}x=&75\\6x+8y=&480\\\end{cases}\Rightarrow E(75, 3.75)\)
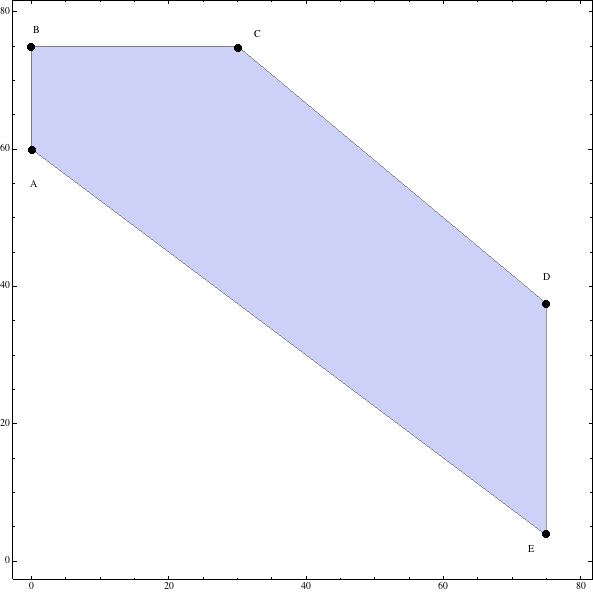
De forma que comprobando por ejemplo con el punto \((0,0)\) se dibuja la región será
Sustituyendo los valores de los vértices de la región obtenida en la función objetivo \(F(x,y)=x+1,2y\), se obtienen los siguientes resultados
\(\displaystyle\begin{cases}F(0,60)=&72\\F(0,75)=&90\\F(30,75)=&120\\F(75, 37.5)=&120\\F(75, 3.75)=&79,5\\\end{cases}\)
Luego, \(F(x,y)\) alcanza el valor mínimo en el punto \(A(0,60)\)
Por lo tanto, será necesario \(\bbox[yellow]{\hbox{ comprar }60\hbox{ kg de la pintura }B\hbox{ siendo el coste }72\hbox{ euros}}\)
Ejercicio 2: (3 ptos) Dada la función:
\(f(x)=\begin{cases}2x^2-a&x\leq -1\\ -3x^{2}+b & {-1}\leq x<1\\ \log x+a& x\geq 1\\\end{cases}\)
a) (1 pto) Calcúlense \(a,b\) para que la función sea continua en todos los puntos
b) (1 pto) Para \(a=0,b=3\), represéntese gráficamente la función
c) (1 pto) Para \(a=0,b=3\), calcúlese la integral definida \(\displaystyle\int_{-1}^1f(x)dx\)
a) La función está formada por tres polinomios, luego el único punto de posible discontinuidad es el salto entre estos tres polinomios, \(x=-1\) y \(x=1\) (ver continuidad de funciones)
Para comprobar si la función es continua en dichos puntos se evalúan los límites laterales y la función en los puntos
\(\lim\limits_{x\to -1^{+}}f(x)=\lim\limits_{x\to -1^{+}}(-3x^2+b)=-3(-1)^2+b=-3+b\)
Calculando el otro límite lateral y el valor de la función en el punto, queda
\(\lim\limits_{x\to -1^{-}}f(x)=\lim\limits_{x\to -1^{-}}(2x^2-a)=2-a=f(-1)\)
Luego, para que la función sea continua en \(-1\) se debe cumplir que \(2-a=-3+b\Rightarrow a+b=5\)
Por otra parte, en \(x=1\),
\(\lim\limits_{x\to 1^{+}}f(x)=\lim\limits_{x\to 1^{+}}(\log x+a)=\log 1+a=a=f(1)\)
Calculando el otro límite lateral y el valor de la función en el punto, queda
\(\lim\limits_{x\to 1^{-}}f(x)=\lim\limits_{x\to 1^{-}}(-3x^2+b)=-3.1^2+b=-3+b\)
Luego, para que la función sea continua en \(1\) (y, por tanto, en todo \(\mathbb{R}\)), se debe cumplir que \(a=-3+b\Rightarrow a-b=-3\)
Luego, para que la función sea continua en todos los puntos se tiene que cumplir \(a+b=5\hbox{ y }a-b=-3\Rightarrow\bbox[yellow]{a=1,b=4}\)
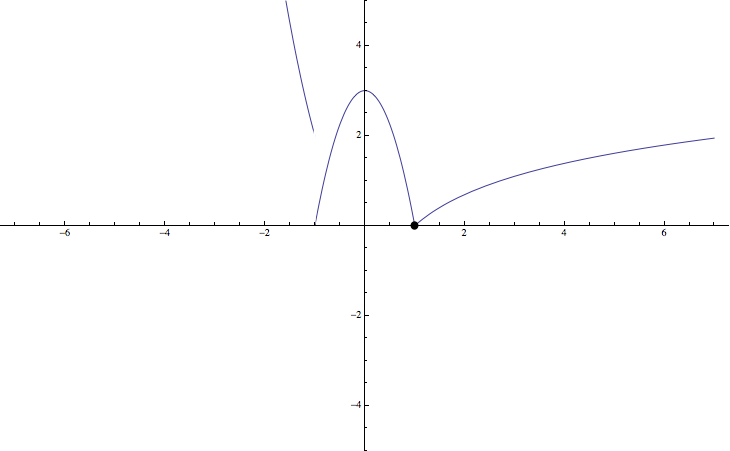
b) La función que se pide representar es
\(f(x)=\begin{cases}2x^2-a&x\leq -1\\ -3x^{2}+b & {-1}\leq x<1\\ \log x+a& x\geq 1\\\end{cases}\)
Para representar la función se seguirán los pasos para dibujar el gráfico de una función
– Como ya se ha comentado, el dominio en este caso serán todos los números reales, ver dominio de una función
– Para calcular el corte con los ejes se iguala la función a cero, ver cómo obtener los cortes con los ejes
\(f(x)=0\Rightarrow 2x^2=0,-3x^2+3=0,\log x=0\Rightarrow x=\pm 1, x=0\), como ni el cero ni el \(-1\) pertenecen a los intervalos en los cuales están los polinomios que anulan, se considerará únicamente el punto de corte \((1,0)\)
Por otra parte, al evaluar \(x=0\) en la función se tiene \(-3.0^2+3=3\), luego se obtiene el punto de corte, \((0,3)\)
Con estos datos y sabiendo que \(2x^2\) y \(-3x^2+3\) son parábolas y recordando la gráfica del logaritmo, ver funciones elementales, es posible dibujar la función
c) Al igual que en el apartado anterior, la función de la cual se pide el área es
\(f(x)=\displaystyle\begin{cases}2x^2&x\leq -1\\ -3x^2+3&-1<x<1\\ \log x+1&x\geq 1\\\end{cases}\)
Consultando la tabla de integrales y recordando cómo se resuelven integrales definidas, se tiene
\(\displaystyle\int_{-1}^1f(x)dx=\displaystyle\int_{-1}^1-3x^2+3dx=\frac{-3x^3}{3}+3x\Big]_{-1}^1=(1^3+3.1)-((-1)^3+3(-1))=4-(-4)=\bbox[yellow]{8}\)
\[\] Ejercicio 3: (2 ptos) Se consideran los siguientes sucesos:
Suceso \(A\): La economía de un cierto país está en recesión
Suceso \(B\): Un indicador económico muestra que la economía de dicho país está en recesión
Se sabe que
\(P(A)=0,005;\qquad\qquad P(B|A)=0,95\qquad\qquad P(\bar{B}|\bar{A})=0,96\)
a) Calcúlese la probabilidad de que el indicador económico muestre que la economía del país no está en recesión y además la economía del país esté en recesión
b) Calcúlese la probabilidad de que el indicador económico muestre que a economía del país está en recesión
a) En este primer caso se pide que suceda a la vez el suceso \(A\) y el complementario de \(B\) (\(\bar{B})\), es decir, consultando la teoría de probabilidad, se tiene
\(P(A\cap\bar{B})=P(A)P(\bar{B}|A)=P(A)P(1-P(B|A))=0,005(1-0,95)=\bbox[yellow]{0,00025}\)
b) La probabilidad pedida será la unión de la probabilidad de que el indicador muestre que la economía está en recesión siendo este dato verídico (es decir, cumpliéndose también \(A\)) más la probabilidad de que el indicador muestre que está en recesión pero que el país no esté en realidad en recesión (es decir, que no se cumpla \(A\), sino su complementario, \(\bar{A}\)
\(P(B)=P((A\cap B)\cup (\bar{A}\cup B))=P(A\cap B)+P(\bar{A}\cap B)=P(A)P(B|A)+P(\bar{A})P(B|\bar{A})=P(A)P(B|A)+(1-P(A))(1-P(\bar{B}|\bar{A}))=0,005.0,95+(1-0,005)(1-0,96)=\bbox[yellow]{0,04455}\)
\[\]Ejercicio 4: (2 ptos) Para estudiar la media de una población con distribución normal de desviación típica igual a \(5\), se ha extraído una muestra aleatoria simple de tamaño \(100\), con la que se ha obtenido el intervalo de confianza \((173,42; 176,56)\) para dicha población
a) Calcúlese la media de la muestra seleccionada
b) Calcúlese el nivel de confianza del intervalo obtenido
a) La media en este caso puede hallarse con la amplitud del intervalo de confianza dado en el enunciado, ver teoría de estadística,
\(\bar{x}=\frac{173,42+176,56}{2}=\bbox[yellow]{174,99}\)
b) El nivel de confianza se puede calcular a partir del error máximo permitido
\(E=\pm z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}\Rightarrow z_{\frac{\alpha}{2}}=\frac{E\sqrt{n}}{\sigma}\), ver teoría de estadística
Por lo tanto, \(z_{\frac{\alpha}{2}}=\frac{1,57\sqrt{100}}{5}=3,14\)
Consultando la tabla de la normal, se obtiene \(1-\frac{\alpha}{2}=0,9992\Rightarrow\alpha=2(1-0,9992)=0,0016\)
De esta manera, el nivel de confianza pedido será \(1-\alpha=1-0,0016=0,9984\Rightarrow\bbox[yellow]{99,84\hbox{%}}\)