OPCIÓN B
\[\]Ejercicio 1: (3 ptos) Se consideran las matrices
\(A\begin{pmatrix}-1 &0&1\\ 3& k&0\\ -k& 1&4\end{pmatrix};\) \(B=\begin{pmatrix}3&1\\ 0& 3\\ 2&0\end{pmatrix}\)
a) Calcúlense los valores de \(k\) para los cuales la matriz \(A\) no tiene inversa
b) Para \(k=0\) calcúlese la matriz inversa \(A^{-1}\)
c) Para \(k=0\) resuélvase la ecuación matricial \(AX=B\)
a) Para que exista \(A^{-1}\), el determinante de \(A\) debe ser no nulo, ver inversa de una matriz. En este caso
\(\begin{array}{|crl|}-1 &0&1\\ 3& k&0\\ -k& 1&4\end{array}=k^2-4k+3=0\Rightarrow k=1\) y \(k=3\)
Es decir, \(\bbox[yellow]{\hbox{para }k=1,3, \hbox{ la matriz no tiene inversa}}\)
b) Para \(k=0\), se tiene
\(A=\begin{pmatrix}-1 &0&1\\ 3& 0&0\\ 0& 1&4\end{pmatrix}\)
El determinante de \(A\) será en este caso \(|A|=0^2-4.0+3=3\), ver cómo calcular determinantes
La inversa de la matriz se calculará con la siguiente fórmula, ver cómo calcular la inversa de una matriz
\(A^{-1}=\frac{(Adj A)^{t}}{|A|}\)
Calculando la matriz de adjuntos y trasponiéndola, se obtiene
\((Adj A)^{t}=\begin{pmatrix}0 &1&0\\ -12& -4&3\\ 3& 1&0\end{pmatrix}\)
Por lo tanto, la inversa será \(\bbox[yellow]{A^{-1}=\frac 13\begin{pmatrix}0 &1&0\\ -12& -4&3\\ 3& 1&0\end{pmatrix}}\)
c) La ecuación tendrá solución cuando sea posible despejar \(X\), es decir, cuando \(A\) tenga inversa ya que \(AX=B\Rightarrow A^{-1}AX=A^{-1}B\Rightarrow X=A^{-1}B\), ver ecuaciones matriciales
Como en el apartado anterior se ha calculado la inversa para \(k=0\), es posible calcular \(X\) en este caso consultando el apartado de cómo multiplicar matrices, se tiene
\(X=BA^{-1}=\frac 13\begin{pmatrix}0 &1&0\\ -12& -4&3\\ 3& 1&0\end{pmatrix}\begin{pmatrix}3&1\\ 0& 3\\ 2&0\end{pmatrix}=\bbox[yellow]{\frac 13\begin{pmatrix}0 &3\\ -30&-21\\ 9&6\end{pmatrix}}\)
Ejercicio 2: (3 ptos) Dada la función: \(f(x)=\displaystyle\begin{cases}\frac ax&x\leq -1\\ \frac{x^2-b}{4}&x>-1\\\end{cases}\)
a) (1 pto) Calcúlense los valores de \(a\) y \(b\) para que la función sea continua y derivable
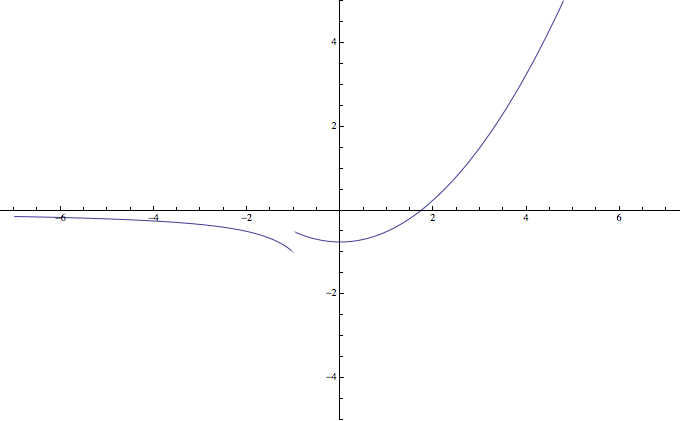
b) (1 pto) Para \(a=1\) y \(b=3\),represéntese la función
c) (1 pto) Calcúlese el valor de \(b\) para que \(\displaystyle\int_0^3 f(x)dx=6\)
a) La función está formada por polinomios, luego el único punto de posible discontinuidad es el salto entre los polinomios, \(x=-1\) (ver continuidad de funciones)
Para comprobar si la función es continua en dicho punto se evalúan los límites laterales y la función en el punto
\(\lim\limits_{x\to -1^{+}}f(x)=\lim\limits_{x\to -1^{+}}\frac{x^2-b}{4}=\frac{1-b}{4}\)
Calculando el otro límite lateral, se tiene
\(\lim\limits_{x\to -1^{-}}f(x)=\lim\limits_{x\to -1^{-}}\frac ax=-a=f(-1)\)
Luego, para que la función sea continua en \(-1\) (y, por tanto, en todo \(\mathbb{R}\)), se debe cumplir que \(-a=\frac{1-b}{4}\)
Para que la función sea derivable tiene que cumplirse que \(f'(-1^{-})=f'(-1^{+})\), ver derivabilidad
En este caso, calculando primeramente la derivada de la función, se tiene
\(f'(x)=\displaystyle\begin{cases}-\frac{a}{x^2}&x\leq -1\\ \frac x2&x>1\\\end{cases}\)
Evaluando \(f'(-1^{-})=f'(-1^{+})\), se tiene que \(-a=\frac 12\Rightarrow a=-\frac 12\), luego, para que la función sea continua y derivable en todos los reales \(\frac 12=\frac{1-b}{4}\Rightarrow\bbox[yellow]{ a=-\frac 12,b=-1 }\)
b) La función a representar será
\(f(x)=\displaystyle\begin{cases}\frac{1}{x}&x\leq -1\\ \frac{x^2-3}{4}&x>1\\\end{cases}\)
Para representar la función se seguirán los pasos para dibujar el gráfico de una función
– El dominio en este caso serán todos los números reales (en el caos del primer trozo de la función, el cero no estaría contenido en el dominio ya que el denominador se anula en este valor, pero como el cero no está en ese primer intervalo, se incluye en el dominio total de la función ), ver dominio de una función
– Para calcular el corte con los ejes se iguala la función a cero, ver cómo obtener los cortes con los ejes
\(f(x)=0\Rightarrow \frac{x^2-3}{4}=0\Rightarrow x=\pm\sqrt{3}\), luego se obtienen los puntos de corte: \((-\sqrt{3},0),(\sqrt{3},0)\)
Por otra parte, al hacer \(x=0\) en la función, se obtiene \((-\frac 34,0)\)
Con estos datos y sabiendo que la función está formada por una hipérbola y una parábola (cuyo vértice es \((-\frac 34,0)\)), ver funciones elementales, es posible dibujar la función
c) Teniendo en cuenta cómo se calcula una integral definida, se tiene
\(6=\displaystyle\int_0^{3}\frac{x^2-b}{4}dx=\frac 14(\frac{x^3}{3}-bx)\Big]_0^3=\frac 14(3^2-b3)\Rightarrow 3b=-15\Rightarrow \bbox[yellow]{b=-5}\)
\[\] Ejercicio 3: (2 ptos) En un cierto punto de una autopista está situado un radar que controla la velocidad de los vehículos que pasan por dicho punto. La probabilidad de que el vehículo que pase por el radar sea un coche es \(0,5\), de que sea un camión es \(0,3\) y de que sea una motocicleta es \(0,2\). La probabilidad de que cada uno de los tres tipos de vehículos supere al pasar por el radar la velocidad máxima permitida es \(0,06\) para un coche, \(0,02\) para un camión y \(0,12\) para una motocicleta. En un momento dado, un vehículo pasa por el radar
a) Calcúlese la probabilidad de que este vehículo supere la velocidad máxima permitida
b) Si un vehículo en cuestión ha superado la velocidad máxima permitida, ¿cuál es la probabilidad de que se trate de una motocicleta?
a) Primeramente se definen las variables a utilizar y los datos:
\(A\equiv\) Por el radar pasa un coche; \(P(A)=0,5\)
\(B\equiv\) Por el radar pasa un coche; \(P(B)=0,3\)
\(C\equiv\) Por el radar pasa un coche; \(P(C)=0,2\)
\(S\equiv\) El vehículo que pasa por el radar supera la velocidad máxima permitida
\(P(S|A)=0,06\) Probabilidad de superar la velocidad máxima si es un coche
\(P(S|B)=0,02\) Probabilidad de superar la velocidad máxima si es un camión
\(P(S|C)=0,12\) Probabilidad de superar la velocidad máxima si es una motocicleta
a) Los vehículos que superan la velocidad máxima pueden ser coches, camiones o motocicletas, por lo tanto, teniendo en cuenta la teoría de la probabilidad, se tiene
\(P(S)=P((A\cap S)\cup (B\cap S)\cup (C\cap S))=P(A\cap S)+P(B\cap S)+P(C\cap S)=P(A)P(S|A)+P(B)P(S|B)+P(C)P(S|C)=0,5.0,006+0,3.0,02+0,2.0,12=\bbox[yellow]{0,06}\)
b) La probabilidad pedida será una probabilidad condicionada, ver probabilidad condicionada,
\(P(C|S)=\frac{P(C\cap S)}{P(S)}=\frac{P(C).P(S|C)}{P(S)}=\frac{0,2.0,12}{0,06}=\bbox[yellow]{0,4}\)
\[\]Ejercicio 4: (2 ptos) Se supone que el precio (en euros) de un refresco se puede aproximar por una variable aleatoria con distribución normal de media \(\mu\) y desviación típica igual a \(0,09\) euros. Se toma una muestra aleatoria simple del precio del refresco en \(10\) establecimientos y resulta:
\(1,50\quad\quad 1,60\quad\quad 1,10\quad\quad 0,90\quad\quad 1,00\quad\quad 1,60\quad\quad 1,40\quad\quad 0,90\quad\quad 1,30\quad\quad 1,20\)
a) Determínese un intervalo de confianza con un nivel del \(95\)% para \(\mu\)
b) Calcúlese el tamaño mínimo que ha de tener la muestra elegida para que el valor absoluto de la diferencia entre la media muestral y \(\mu\) sea menor o igual que \(0,10\) euros con probabilidad mayor o igual que \(0,99\)
a) Considerando \(x\) la variable aleatoria que mide el precio de un refresco, se comportará como una variable continua con distribución Normal, \(x:N(\mu,\sigma)\), ver estadística
El intervalo de confianza se calculará utilizando la siguiente fórmula, ver teoría de estadística,
\(IC=(\bar{x}-z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}},\bar{x}+z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}})\)
Con \(\bar{x}=\frac{\sum x_i}{n}=\frac{1,50+1,60+1,10+0,90+1,00+1,60+1,40+0,90+1,30+1,20}{10}=1,25\)
El valor de \(z_{\frac{\alpha}{2}}\) se obtiene a partir del nivel de confianza dado en el enunciado y consultando la tabla de la normal
Nivel de confianza del \(95\hbox{%}\Rightarrow 1-\alpha=0,95\Rightarrow \alpha=0,05\Rightarrow z_{\frac{\alpha}{2}}=1,96\)
Por lo tanto,
\(IC=(1,25-1,96\frac{0,09}{\sqrt{10}},1,25+1,96\frac{0,09}{\sqrt{10}})=\bbox[yellow]{(1,19, 1,31)}\)
b) El tamaño muestral es posible obtenerlo a partir del error máximo permitido
\(E=\pm z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}\Rightarrow n=(z_{\frac{\alpha}{2}}\frac{\sigma}{E})^2\), ver teoría de estadística
En este caso, al ser \(99\)% el nivel de confianza, \(1-\alpha=0,99\Rightarrow\alpha=0,01\), y consultando la tabla de la normal, se tiene \(z_{\frac{\alpha}{2}}=2,58\), por lo tanto, \(n>(2,58\frac{0,09}{0,1})^2=5,39\Rightarrow\bbox[yellow]{n\geq 6}\)