OPCIÓN A
\[\]Ejercicio 1: (2 ptos) Se consideran las matrices
\(A=\begin{pmatrix}0 &2\\ 3& 0\end{pmatrix}\) y \(B=\begin{pmatrix}-3 &8\\ 3& -5\end{pmatrix}\)
a) Calcúlense \(A^{-1}\)
b) Resuélvase el sistema de ecuaciones dado por \(AX=B-I\), donde \(I\) es la matriz identidad
a) Para que exista \(A^{-1}\), el determinante de \(A\) debe ser no nulo, ver inversa de una matriz
En este caso, \(\begin{array}{|crl|}0 &2\\ 3& 0\end{array}=0-6=-6\)
La inversa de la matriz se calculará con la siguiente fórmula, ver cómo calcular la inversa de una matriz
\(A^{-1}=\frac{(Adj A)^{t}}{|A|}\)
Calculando la matriz de adjuntos y trasponiéndola, se obtiene
\((Adj A)^{t}=\begin{pmatrix}0 &-2\\ -3&0\end{pmatrix}\)
Por lo tanto, la inversa será \(\bbox[yellow]{A^{-1}=\begin{pmatrix}0 &\frac 13\\ \frac 12&0\end{pmatrix}}\)
b) La ecuación tendrá solución cuando sea posible despejar \(X\), es decir, cuando \(A\) tenga inversa ya que denotando \(X=\begin{pmatrix}x\\ y\\ z\end{pmatrix}\) y sabiendo que \(I=\begin{pmatrix}1&0\\ 0&1\end{pmatrix}\), se tiene
\(AX=B-I\Rightarrow A^{-1}AX=A^{-1}(B-I)\Rightarrow X=A^{-1}(B-I)\), ver ecuaciones matriciales
Como en el apartado anterior se ha calculado la inversa, es posible calcular \(X\) en este caso consultando el apartado de cómo multiplicar matrices, se tiene
\(X=A^{-1}(B-I)=\begin{pmatrix}0 &\frac 13\\ \frac 12&0\end{pmatrix}\Big[\begin{pmatrix}-3 &8\\ 3& -5\end{pmatrix}-\begin{pmatrix}1&0\\ 0&1\end{pmatrix}\Big]=\bbox[yellow]{\begin{pmatrix}1&-2\\ -2& 4\end{pmatrix}}\)
Ejercicio 2: (2 ptos) Sea \(C\) la región del plano delimitada por el sistema de ecuaciones
\(\begin{cases}x+3y\geq&3\\2x-y\leq&4\\2x+y\leq&24\\x\geq 0,&y\geq 0\\\end{cases}\)
a) Represéntese la región \(C\) y calcúlense las coordenadas de sus vértices
b) Determínese el punto de \(C\) donde la función \(f(x,y)=3x+y\) alcanza su valor máximo. Calcúlese dicho valor
a) Para obtener los vértices de la región pedida, se resuelven las ecuaciones dos a dos, ver cómo resolver problemas de programación lineal y consultar cómo resolver sistemas de ecuaciones se obtiene el resultado
\(\displaystyle\begin{cases}2x-y=&4\\2x+y=&24\\\end{cases}\Rightarrow A(7,10)\)
\(\displaystyle\begin{cases}2x-y=&4\\x+3y=&3\\\end{cases}\Rightarrow B(\frac{15}{7},\frac 27)\)
\(\displaystyle\begin{cases}y=&0\\x+3y=&3\\\end{cases}\Rightarrow C(3,0)\)
y
\(\displaystyle\begin{cases}y=&0\\2x+y=&24\\\end{cases}\Rightarrow D(12,0)\)
De forma que los vértices de la región pedida serán \(\bbox[yellow]{A(7,10),\;B(\frac{15}{7},\frac 27),\;C(3,0)\;y\;D(12,0)}\)
Y la región será
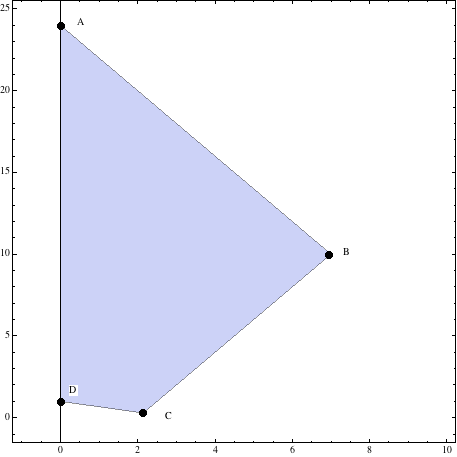
2. Sustituyendo los valores de los vértices de la región obtenida en la función objetiva \(f(x,y)\), se obtienen los siguientes resultados
\(\displaystyle\begin{cases}f(7,10)=&31\\f(\frac{15}{7},\frac 27)=&\frac{47}{7}\\f(3,0)=&9\\f(12,0)=&36\\\end{cases}\)
Luego, \(f(x,y)\) alcanza el valor máximo en el punto \(\bbox[yellow]{D(12,0)\;\hbox{y vale }36}\)
\[\] Ejercicio 3: (2 ptos) Se considera la función real de variable real definida por
\(f(x)=\frac{x^3}{x^2-9}\)
se pide:
a) (1 pto) Hallar las asíntotas de su gráfica
b) (1 pto) Hallar la ecuación de la recta tangente a la gráfica de \(f(x)\) en el punto de abscisa \(x=1\)
a) Para estudiar las asintótas de la función, consultar el apartado de teoría de asíntotas
. Asintótas verticales:
Las posibles asíntotas verticales estarían en los puntos que no están en el dominio, ver cómo se calcula el dominio de una función. En este caso, como el denominador se anula en \(x=\pm 3\), éstos serán los puntos de posible asíntotas verticales
\(\lim\limits_{x\to -3^{-}}\frac{x^3}{x^2-9}=\frac{-27}{0^{+}}=-\infty\)
y
\(\lim\limits_{x\to -3^{+}}\frac{x^3}{x^2-9}=\frac{-27}{0^{-}}=\infty\)
Por lo tanto, \(\bbox[yellow]{x=-3}\) será una asíntota vertical
Por otra parte, \(\lim\limits_{x\to 3^{-}}\frac{x^3}{x^2-9}=\frac{27}{0^{-}}=-\infty\)
y
\(\lim\limits_{x\to 3^{+}}\frac{x^3}{x^2-9}=\frac{-27}{0^{+}}=\infty\)
Por lo tanto, \(\bbox[yellow]{x=3}\) será una asíntota vertical
. Asintótas horizontales:
Consultando cómo se resuelven límites y utilizando la Regla de L’Hôpital se tiene que
\(\lim\limits_{x\to\pm\infty}\frac{x^3}{x^2-9}=\pm\infty\)
Luego, \(\bbox[yellow]{\hbox{no hay horizontales }}\)
. Asintótas oblicuas:
Las posibles asíntotas oblicuas tendrían la siguiente expresión \(y=mx+n\)
Con \(m=\lim\limits_{x\to\pm\infty}\frac{f(x)}{x}=\lim\limits_{x\to\pm\infty}\frac{\frac{x^3}{x^2-9}}{x}=\lim\limits_{x\to\pm\infty}\frac{x^3}{x^3-9x}=1\)
Y \(n=\lim\limits_{x\to\pm\infty}(f(x)-mx)=\lim\limits_{x\to\pm\infty}(\frac{x^3}{x^2-9}-x)=\lim\limits_{x\to\pm\infty}\frac{9x}{x^2-9}=0\)
Luego, la recta \(\bbox[yellow]{y=x}\) será asíntota oblicua
b) La ecuación de la recta tangente en \(x=1\) viene dada por la siguiente ecuación, ver ecuaciones de la recta
\(y-f(1)=f'(1)(x-1)\)
Primeramente se calculará el valor de la función en el punto pedido, \(f(1)=\frac{1^3}{1^2-9}=-\frac 18\) y la derivada de la función, ver la tabla de derivadas
\(f'(x)=\displaystyle\frac{3x^2(x^2-9)-x^3.2x}{(x^2-9)^2}=\frac{x^4-27x^2}{(x^2-9)^2}\)
Luego, \(f'(1)=\frac{1^4-27.1^2}{(1^2-9)^2}=-\frac{13}{32}\)
Por lo tanto, se tendrá el resultado \(y-(-\frac 18)=-\frac{13}{32}(x-1)\Rightarrow\bbox[yellow]{y=-\frac{13}{32}x+\frac{9}{32}}\)
\[\]Ejercicio 4: (2 ptos) En un avión de línea regular existe clase turista y clase preferente. La clase turista ocupa las dos terceras partes del pasaje y la clase preferente, el resto. Se sabe que todos los pasajeros que viajan en la base preferente saben hablar inglés y que el \(40\)% de los pasajeros que viajan en clase turista no saben hablar inglés. Se elige un pasajero del avión al azar
a) Calcúlese la probabilidad de que el pasajero elegido sepa hablar inglés
b) Si se observa que el pasajero elegido sabe hablar inglés, ¿cuál es la probabilidad de que viaje en la clase turista?
a) Para resolver el problema se definen las variables a utilizar:
\(T\equiv\) El pasajero viaja en clase turista
\(P\equiv\) El pasajero viaja en clase preferente
\(I\equiv\) El pasajero sabe hablar inglés
Los datos que da el enunciado son los siguientes
\(P(T)=\frac 23\)
\(P(P)=\frac 13\)
\(P(I|P)=1\)
\(P(\bar{I}|T)=0,40\)
Hay que tener en cuenta también que saber inglés viajando en clase turista \((I|T)\) y no saber inglés si viaja en turista \((\bar{I}|T)\) son complementarios, \(P(I|T)=1-P(\bar{I}|T)=1-0,40=0,60\)
a) La probabilidad de que sepa inglés será la probabilidad de que sepa inglés viajando en clase turista más la probabilidad de que lo sepa viajando en clase preferente, ver la teoría de la probabilidad
\(P(I)=P((T\cap I)\cup (P\cap I))=P(T\cap I)+P(P\cap I)=P(T)P(I|T)+P(P)P(I|P)\)
Luego, \(P(I)=\frac 23.0,60+\frac 13.1=\frac{11}{15}=\bbox[yellow]{0,7333}\)
b) Suponiendo que el cliente habla inglés, la probabilidad de que viaje en clase turista será una probabilidad condicionada, ver probabilidad condicionada,
\(P(T|I)=\frac{P(T\cap I)}{P(I)}=\frac{P(T).P(I|T)}{P(I)}=\frac{\frac 23.0,6}{\frac{11}{15}}=\bbox[yellow]{0,5455}\)
\[\]Ejercicio 5: (2 ptos) El tiempo de renovación de un teléfono móvil, expresado en años, se puede aproximar mediante una distribución normal con desviación típica de \(0,4\) años
a) Se toma una muestra aleatoria simple de \(400\) usuarios y se obtiene una media muestral igual a \(1,75\) años. Determínese un intervalo de confianza al \(95\)% para el tiempo medio de renovación de un teléfono móvil
b) Determínese el tamaño muestral mínimo necesario para que el valor absoluto de la diferencia entre la media muestral y la media poblacional sea menor o igual a \(0,02\) años con un nivel de confianza del \(90\)%
a) Considerando \(x\) la variable aleatoria que mide el tiempo de renovación de un teléfono móvil, se comportará como una variable continua con distribución Normal, \(x:N(\mu,\sigma)\), ver estadística
Para muestras de \(400\) elementos, las medias muestrales también siguen una distribución Normal del tipo \(\bar{x}:N(\mu,\frac{\sigma}{\sqrt{n}})\)
El intervalo de confianza se calculará utilizando la siguiente fórmula, ver teoría de estadística,
\(IC=(\bar{x}-z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}},\bar{x}+z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}})\)
El valor de \(z_{\frac{\alpha}{2}}\) se obtiene a partir del nivel de confianza dado en el enunciado y consultando la tabla de la normal
Nivel de confianza del \(95\hbox{%}\Rightarrow 1-\alpha=0,95\Rightarrow \alpha=0,05\Rightarrow z_{\frac{\alpha}{2}}=1,96\)
Por lo tanto,
\(IC=(1,75-1,96\frac{0,4}{\sqrt{400}},1,75+1,96\frac{0,4}{\sqrt{400}})=\bbox[yellow]{(1,71, 1,79)}\)
b) El tamaño muestral es posible obtenerlo a partir del error máximo permitido
\(E=\pm z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}\Rightarrow n=(z_{\frac{\alpha}{2}}\frac{\sigma}{E})^2\), ver teoría de estadística
En este caso, al ser \(90\)% el nivel de confianza, \(1-\alpha=0,90\Rightarrow\alpha=0,10\), y consultando la tabla de la normal, se tiene \(z_{\frac{\alpha}{2}}=1,645\), por lo tanto, \(n>(1,645\frac{0,4}{0,02})^2\Rightarrow\bbox[yellow]{n\geq 1083}\)
Ir a la Opción B de este examen