Definición

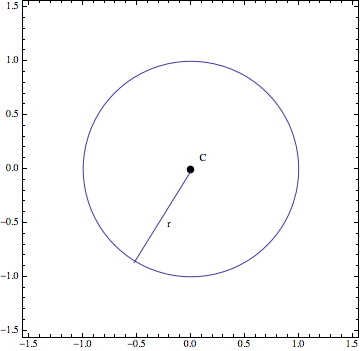
La circunferencia es una curva plana cerrada cuyos puntos equidistan (están todos a la misma distancia: el radio \(r\)) de un punto fijo llamado centro, \(C\). El interior de la circunferencia y la propia circunferencia forman un círculo

Ecuación general de la circunferencia (centrada en el origen): \(\bbox[yellow]{x^2+y^2+mx+ny+p=0}\)

Centro de la circunferencia: \(C=C(a,b)\)

Punto del que equidistan todos los puntos de la circunferencia
Puede calcularse a partir de la expresión general de la circunferencia

\(m=-2a\Rightarrow \bbox[yellow]{a=-\frac m2}\)
\(n=-2b\Rightarrow \bbox[yellow]{b=-\frac n2}\)

Radio de la circunferencia: \(r\)

Segmento que une el centro de la circunferencia con un punto cualquiera de la misma
Puede calcularse también con los datos de la expresión general de la circunferencia

\(p=a^2+b^2-r^2\Rightarrow\bbox[yellow]{r=\sqrt{p-a^2-b^2}}\)

 

Diamétro de la circunferencia: \(d=2r\)

Segmento que va de lado a lado de la circunferencia pasando por el centro

 

Cuerda de la circunferencia

Segmento que va de lado a lado de la circunferencia sin pasar por el centro

 

Gráfica de una circunferencia

 

 

Volver a cónicas                                                                                                             Ver ejercicios de cónicas