Ejercicio : (Junio 2011 Opción A) (Calificación: 2 ptos)
a) (1 pto) Calcular la integral \(\displaystyle\int_1^3x\sqrt{4+5x^2}dx\)
b) (1 pto) Hallar los valores mínimo y máximo absolutos de la función \(f(x)=\sqrt{12-3x^2}\)
a) Consultando la tabla de integrales y recordando cómo se resuelven integrales definidas, se tiene
\(\displaystyle\int_1^3x\sqrt{4+5x^2}dx=\displaystyle\int_1^3 x(4+5x^2)^{\frac 12}dx=\frac{1}{10}\frac{(4+5x^2)^{\frac 32}}{\frac 32}\Big]_1^3=\bbox[yellow]{\frac{1}{15}(7^3-3^3)}\)
b) Para calcular los máximos y mínimos de la función, se derivará y se igualará a cero su derivada, ver cómo calcular máximos y mínimos de una función y también consultar la tabla de derivadas
En este caso, \(f'(x)=\frac 12(12-3x^2)^{-\frac 12}(-6x)=\frac{-6x}{2\sqrt{12-3x^2}}=0\Rightarrow x=0\)
Luego, el punto crítico es \(x=0\) y evaluando el signo de la derivada antes y después de dicho punto, se tiene que \(f'(x<0)<0\) y \(f'(x>0)>0\), por lo tanto, sabiendo que \(f(0)=2\), el máximo estará en \(\bbox[yellow]{(0,\sqrt{2})}\)
El dominio de la función serán todos los números que hagan que el polinomio de dentro de la raíz sea positivo, ver dominio de una función, en este caso \(12-3x^2\geq 0\Rightarrow x\geq 2\) y \(x\leq 2\), es decir, el dominio será \(x\in [-2,2]\)
La función es una parábola hacia abajo con vértice en \((0,\sqrt{2})\), ver funciones elementales, por lo que sus mínimos serán los puntos que cortan al eje \(OX\), es decir, sus mínimos (en el dominio en el que está definida) serán \(\bbox[yellow]{(-2,0), (2,0)}\)
Ejercicio : (Junio 2011 Opción A) (Calificación:2 ptos)
a) (1 pto) Calcular el siguiente límite \(\lim\limits_{x\to +\infty}\frac{\sqrt{x}}{\sqrt{x+\sqrt{x}}}\)
b) (1 pto) Demostrar que la ecuación \(4x^5+3x+m=0\) sólo tiene una raíz real, cualquiera que sea el número \(m\). Justificar la respuesta indicando qué teoremas se usan
a) \(\lim\limits_{x\to +\infty}\frac{\sqrt{x}}{\sqrt{x+\sqrt{x}}}=\frac{\infty}{\infty}\)
De manera que se obtiene una indeterminación (ver indeterminaciones), para resolver el límite se dividirá entre la raíz de \(x\) arriba y abajo de la fracción, ver cómo resolver límites
\(\lim\limits_{x\to +\infty}\frac{\sqrt{x}}{\sqrt{x+\sqrt{x}}}=\lim\limits_{x\to +\infty}\frac{\frac{\sqrt{x}}{\sqrt{x}}}{\frac{\sqrt{x+\sqrt{x}}}{\sqrt{x}}}=\lim\limits_{x\to +\infty}\frac{1}{\sqrt{1+\frac{1}{\sqrt{x}}}}=\bbox[yellow]{1}\)
b) Para probar que la ecuación tiene al menos una solución real, se aplicará el \(\bbox[yellow]{\hbox{Teorema de Bolzano}}\) a la función \(f(x)=4x^5+3x+m\), ver teoremas fundamentales
Como la función es polinómica, será continua en todos los números reales, ver continuidad de una función
La función cambia de signo entre \(-\infty\) y \(\infty\), luego, por el Teorema de Bolzano, existe un \(c\in (-\infty,\infty)\) tal que \(f(c)=0\), luego \(c\) será una solución de \(4x^5+3x+m=0\)
Para probar que dicha solución es, de hecho, única, se usará el \(\bbox[yellow]{\hbox{Teorema de Rolle}}\), ver teoremas fundamentales
Dicho teorema dice que siendo \(f(x)\) continua en el intervalo \([a,b]\) y derivable en \((a,b)\), si \(f(a)=f(b)\), entonces existe un punto \(c\in (a,b)\) tal que \(f'(c)=0\)
Al ser polinómica, \(f(x)\) es continua y derivable en todos los números reales, ver continuidad y derivabilidad
De forma que, suponiendo que existen dos puntos \(a\) y \(b\) tal que \(f(a)=f(b)\), por el Teorema de Rolle, debería existir un punto \(c\) en el intervalo \((a,b)\) tal que anulara su derivada
La derivada viene dada como, ver tabla de derivadas, \(f'(x)=20x^4+3=0\Rightarrow x=(-\frac{3}{20})^{\frac 14}\notin\mathbb{R}\)
Luego, como no existe un punto que anule la derivada, no existen dos puntos tales que \(f(a)=f(b)=0\) (no existen dos soluciones de \(f(x)\)), y por lo tanto la solución de \(f(x)\) tiene que ser única
Ejercicio : (Junio 2011 Opción B) (Calificación: 3 ptos)
Dada la función \(f(x)=\frac{ax^4+1}{x^3}\)
a) (1 pto)Determinar el valor de \(a\)para el que la función posee un mínimo relativo en \(x=1\). Para ese valor de \(a\), obtener los otros puntos en que \(f\) tiene un extremo relativo
b) (1 pto) Obtener las asíntotas de la gráfica de \(y=f(x)\) para \(a=1\)
c) (1 pto) Esbozar la gráfica de la función para \(a=1\)
a) Para que la función tenga un mínimo en \(x=1\), tiene que cumplirse que la derivada en ese punto sea cero, ver máximos y mínimos y consultar también la tabla de derivadas
\(f'(x)=\frac{4ax^3.x^3-(ax^4+1)3x^2}{(x^3)^2}\Rightarrow \frac{4ax^4-3ax^4-3}{x^4}\Rightarrow \frac{ax^4-3}{x^4}\Rightarrow f'(1)=\frac{a-3}{1}=0\Rightarrow a=3\)
Para saber si con ese valor de \(a\), \(x=1\) es un mínimo, se evalúa \(x=1\) en la segunda derivada,
\(f»(x)=\frac{12x^3.x^4-(3x^4-3)4x^3}{(x^4)^2}=\frac{12}{x^5}\)
Sustituyendo \(x=1\), se tiene que \(f»(1)=12>0\). Luego, en \(x=1\) hay, efectivamente, un mínimo y, por lo tanto, el resultado será \(\bbox[yellow]{a=3}\)
b) Para estudiar las asintótas de la función, consultar el apartado de teoría de asíntotas
. Asintótas verticales:
Las posibles asíntotas verticales estarían en los puntos que no están en el dominio, ver cómo se calcula el dominio de una función. En este caso, el denominador se anula en \(x=0\) y consultando cómo resolver límites, se tiene
\(\lim\limits_{x\to 0^{-}}\frac{x^4+1}{x^3}=-\infty\)
\(\lim\limits_{x\to 0^{+}}\frac{x^4+1}{x^3}=\infty\)
Luego, hay una asíntota vertical en \(\bbox[yellow]{x=0}\)
. Asintótas horizontales:
Consultando cómo se resuelven límites se tiene que
\(\lim\limits_{x\to\pm\infty}\frac{x^4+1}{x^3}=\infty\)
Luego, \(\bbox[yellow]{\hbox{no hay horizontales}}\)
. Asintótas oblicuas:
Las posibles asíntotas oblicuas tendrían la siguiente expresión \(y=mx+n\)
Con \(m=\lim\limits_{x\to\pm\infty}\frac{f(x)}{x}=\lim\limits_{x\to\pm\infty}\frac{\frac{x^4+1}{x^3}}{x}=1\)
Y \(n=\lim\limits_{x\to\pm\infty}(f(x)-mx)=\lim\limits_{x\to\pm\infty}(\frac{x^4+1}{x^3}-x)=\lim\limits_{x\to\pm\infty}\frac{x^4+1-x^4}{x^3}=\lim\limits_{x\to\pm\infty}\frac{1}{x^3}=0\)
Luego, la recta \(\bbox[yellow]{y=x}\) será asíntota oblicua
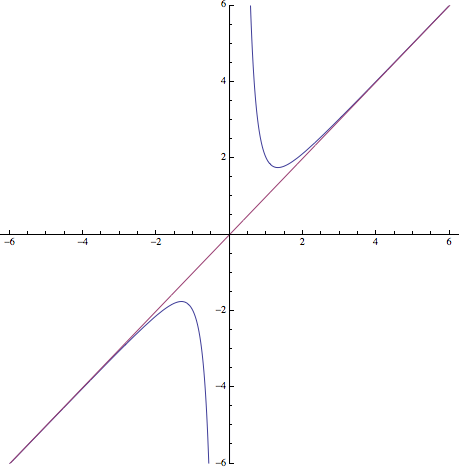
c) Para representar la función se seguirán los pasos para dibujar el gráfico de una función
– El dominio en este caso serán todos los números reales menos el cero ya que el denominador sólo se anula en este valor, ver dominio de una función
– Para calcular el corte con los ejes se iguala la función a cero, ver cómo obtener los cortes con los ejes
\(f(x)=0\Rightarrow x=\pm (-1)^{\frac 14}\Rightarrow\hbox{Imposible}\), luego la función no cortará a \(y=0\)
Por otra parte, como el cero no está en el dominio, la función tampoco cortará a \(x=0\)
Con estos datos y los obtenidos en los apartados anteriores, es posible dibujar la función
Ejercicio : (Junio 2010 Opción A) (Calificación: 3 ptos)
Dada la función \(f(x)=\frac{x^2+2}{x^2+1}\)
se pide:
a) (0,75 ptos) Estudiar los intervalos de crecimiento y decrecimiento de \(f(x)\)
b) (0,75 ptos) Hallar los puntos de inflexión de la gráfica de \(f(x)\)
c) (0,75 ptos) Hallar las asíntotas y la gráfica de \(f(x)\)
d) (0,75 ptos) Hallar el área del recinto acotado que limitan la gráfica de \(f(x)\), el eje de abscisas y las rectas \(y=x+2,x=1\)
a) Los intervalos de crecimiento y decrecimiento se estudiarán calculando los máximos y mínimos de la función, ver máximos y mínimos y la tabla de derivadas
\(f'(x)=\frac{2x(x^2+1)-(x^2+2)2x}{(x^2+1)^2}=0\Rightarrow \frac{2x^3+2x-2x^3-4x}{(x^2+1)^2}=0\Rightarrow \frac{-2x}{(x^2+1)^2}=0\Rightarrow -2x=0\Rightarrow x=0\)
Para saber si el punto crítico obtenido es máximo o mínimo, se evalúa en la segunda derivada,
\(f»(x)=\frac{(x^2+1)(-2(x^2+1)+8x^2)}{(x^2+1)^4}=\frac{6x^2-2}{(x^2+1)^3}\)
Sustituyendo el valor obtenido, \(x=0\), se tiene que \(f»(0)=-2<0\)
De esta forma, consultando cómo saber si los puntos críticos son máximos o mínimos, se concluye que (sabiendo que \(f(0)=2\)) la función tiene un \(\bbox[yellow]{\hbox{máximo en }(0,2)}\)
b) Para hallar los puntos de inflexión de \(f(x)\), se estudia la curvatura de la función, para ello se iguala la segunda derivada a cero (hallada en el apartado anterior), ver cómo estudiar la curvatura de una función y consultar también cómo resolver polinomios
\(f»(x)=\frac{6x^2-2}{(x^2+1)^3}=0\Rightarrow x=\pm\frac{\sqrt{3}}{3}\)
Para saber cómo cambia la curvatura de la función en los puntos obtenidos, se evalúa la segunda derivada antes y después de dichos puntos
\(f»(x<-\frac{\sqrt{3}}{3})>0, f»(\frac{\sqrt{3}}{3}>x>-\frac{\sqrt{3}}{3})<0, f»(x>\frac{\sqrt{3}}{3})>0\). Por lo tanto, ver cómo estudiar la curvatura de una función, se tiene que la función antes de \(-\frac{\sqrt{3}}{3}\) será cóncava, entre \(-\frac{\sqrt{3}}{3}\) y \(\frac{\sqrt{3}}{3}\) será convexa y después de \(\frac{\sqrt{3}}{3}\) será cóncava de nuevo
De forma que sustituyendo en la función el valor obtenido al igualar la segunda derivada a cero, los puntos de inflexión serán \(\bbox[yellow]{(-\frac{\sqrt{3}}{3},\frac 74),(\frac{\sqrt{3}}{3},\frac 74)}\)
c) Para estudiar las asintótas de la función, consultar el apartado de teoría de asíntotas
. Asintótas verticales:
Las posibles asíntotas verticales estarían en los puntos que no están en el dominio, ver cómo se calcula el dominio de una función. En este caso, como el denominador no se anula en ningún punto real \(x^2+2=0\Rightarrow x=\sqrt{-2}\), \(\bbox[yellow]{\hbox{no hay verticales}}\)
. Asintótas horizontales:
Consultando cómo se resuelven límites y utilizando la Regla de L’Hôpital se tiene que
\(\lim\limits_{x\to\infty}\frac{x^2+2}{x^2+1}=1\)
Luego, hay una asíntota horizontal en \(\bbox[yellow]{\hbox{horizontales }\equiv y=1}\)
. Asintótas oblicuas:
Como hay asíntotas horizontales, \(\bbox[yellow]{\hbox{no hay oblicuas}}\), ver la teoría de asíntotas
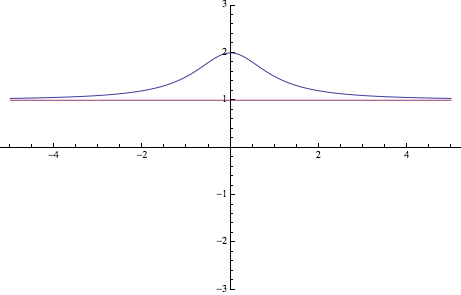
Para representar la función se seguirán los pasos para dibujar el gráfico de una función
– Como ya se ha comentado, el dominio en este caso serán todos los números reales ya que el denominador no se anula para ningún valor real
– Para calcular el corte con los ejes se iguala la función a cero, ver cómo obtener los cortes con los ejes
\(f(x)=0\Rightarrow \hbox{Imposible}\), luego la función no cortará a \(y=0\)
Por otra parte, como \(f(0)=2\), se obtiene el punto de corte, \((0,2)\)
Con estos datos y los obtenidos en los apartados anteriores, es posible dibujar la función
c) Para hallar el área pedida, se calculará la integral definida de la resta entre \(f(x)\) y \(y=x+2\), ver cómo se calcula una integral definida
Para saber los límites de la integral, se estudian los puntos de cortes de ambas funciones,
\(\frac{x^2+2}{x^2+1}=x+2\Rightarrow x=0\)
De forma que los límites de la integral serán \(0\) y \(1\), consultando la tabla de integrales es posible obtener el resultado pedido
\(A=\displaystyle\int_0^1(x+2-\frac{x^2+2}{x^2+1})dx=\int_0^1(x+1-\frac{1}{x^2+1})dx=(\frac{x^2}{2}+x-\arctan x\Big]_0^1=\bbox[yellow]{\frac 32-\frac{\pi}{4}}\)
Ver más ejercicios de Análisis en Selectividad

