OPCIÓN A
\[\]Ejercicio 1: (2 ptos)
Considérese el siguiente sistema de ecuaciones dependiente del parámetro real \(\lambda\):
\(\displaystyle\begin{cases}2x-\lambda y+z=-\lambda&\\4x-2\lambda y+2z=\lambda -3&\\\end{cases}\)
a) Determínense los valores del parámetro real \(\lambda\) que hacen que el sistema sea incompatible
b) Resuélvase el sistema para \(\lambda=1\)
a) Para discutir el sistema de ecuaciones, primeramente se calcula el rango de la matriz asociada al sistema así como el rango de la matriz ampliada, consultar el estudio de un sistema de ecuaciones a través del rango de la matriz asociada. Como en este caso la matriz \(A\) es de \(2×3\), el rango de \(A\) y de \(A^{*}\) no puede ser mayor que dos y es suficiente con buscar los menores \(2×2\) e igualar sus determinantes a cero.
Los únicos menores cuyo determinante está escrito en función del parámetro \(\lambda\) son los siguientes (el resto de menores \(2×2\) tienen determinante cero), recordar cómo se resuelven determinantes:
\(\begin{array}{|crl|}2 &-\lambda\\ 4& \lambda -3\end{array}=3\lambda -3= 0\Rightarrow \lambda -1=0\Rightarrow \lambda= 1\)
\(\begin{array}{|crl|}-\lambda &-\lambda\\ -2\lambda& \lambda -3\end{array}=3\lambda(1-\lambda)= 0\Rightarrow \lambda=0, \lambda= 1\)
y
\(\begin{array}{|crl|}1 &-\lambda\\ 2& \lambda -3\end{array}=3\lambda -3= 0\Rightarrow \lambda -1=0\Rightarrow \lambda= 1\)
Por lo tanto,
– Si \(\lambda\neq 1\), \(\Rightarrow\hbox{El rango de }A=1\neq\hbox{ el rango de }A^{*}=2\Rightarrow\bbox[yellow]{\hbox{el sistema es incompatible si }\lambda\neq 1}\)
– Si \(\lambda=1\), \(\Rightarrow\hbox{ el rango de }A =\neq\hbox{ el rango de }A^{*}=1\Rightarrow\hbox{si }\lambda=1,\hbox{El sistema es compatible indeterminado}\)
b) Para \(\lambda=1\), el sistema es compatible indeterminado, así que tendrá infinitas soluciones y se puede resolver dando dos parámetro como valores a dos de las incógnitas y escribiendo la otra en función de dichos parámetros.
\(\displaystyle\begin{cases}2x-y+z=-1&\\4x-2y+2z=-2&\\\end{cases}\)
Dando a la \(x\) el valor \(\nu\) y a la \(z\) el valor \(\mu\), se tiene el resultado \(\bbox[yellow]{x=\nu,\;\; y=1+2\nu+\mu,\;\; z=\mu}\)
Ejercicio 2: (2 ptos) Se considera la función real de variable real definida por \(\frac{(x-3)^2}{x(x-2)}\)
1. Determínense las asíntotas de \(f\)
2. Estúdiese si la función \(f\) es creciente o decreciente en un entorno de \(x = 4\)
1. Para estudiar las asintótas de la función conviene consultar el apartado de teoría de asíntotas
. Asíntotas verticales:
Las posibles asíntotas verticales estarían en los puntos que no están en el dominio, ver cómo se calcula el dominio de una función. En este caso, los únicos puntos reales en los que no está definida la función son \(0 y 2\)
Para comprobar si en esos puntos hay asíntotas se calculan los límites laterales de la función.
\(\lim\limits_{x\to 2^{-}}\frac{(x-3)^2}{x(x-2)}=-\infty\)
\(\lim\limits_{x\to 2^{+}}\frac{(x-3)^2}{x(x-2)}=\infty\)
y
\(\lim\limits_{x\to 0^{-}}\frac{(x-3)^2}{x(x-2)}=\infty\)
\(\lim\limits_{x\to 0^{+}}\frac{(x-3)^2}{x(x-2)}=-\infty\)
Luego, hay asíntotas verticales en \(\bbox[yellow]{x=0, x=2}\)
. Asíntotas horizontales:
\(\lim\limits_{x\to\pm\infty}f(x)=1\), luego hay una asíntota horizontal en \(\bbox[yellow]{y=1}\)
. Asíntotas oblicuas:
Como hay asíntotas horizontales, \(\bbox[yellow]{\hbox{no hay oblicuas}}\), ver la teoría de asíntotas
2. Los intervalos de crecimiento y decrecimiento se estudiarán calculando los máximos y mínimos de la función, ver máximos y mínimos, la tabla de derivadas y consultar también cómo resolver polinomios
\(f'(x)=\frac{2(x-3)(2x-3)}{x^2(x-2)^2}=0\Rightarrow x=3, x=\frac 32\)
La derivada es positiva antes del punto \(x=\frac 32\) y después del \(x=3\)
Entre \(\frac 32 y 3\), \(f'(x)\) es negativa, luego la función \(f\) crecerá en los intervalos \((-\infty, \frac 32)\cup (3,\infty)\) y decrecerá en \((\frac 32, 3)\)
Como \(x=4\) está en el intervalo \((3,\infty)\), la función será \(\bbox[yellow]{\hbox{creciente en un entorno de } x=4}\)
\[\] Ejercicio 3: (2 ptos)
Se considera la función real de variable real definida por \(f(x) = 2e^{x+1}\)
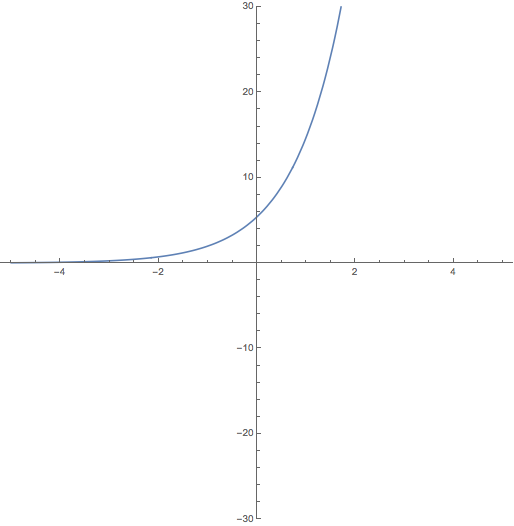
1. Esbócese la gráfica de la función \(f\)
2. Calcúlese el área del recinto plano acotado limitado por la gráfica de
la función, el eje de abscisas y las rectas \(x = 0\) y \(x = 1\)
Para representar la función se seguirán los pasos para dibujar el gráfico de una función
– El dominio de la función serán todos los números reales, ver cómo calcular el dominio de una función
– Para calcular el corte con los ejes se iguala la función a cero y se iguala también \(x\) a cero, ver cómo obtener los cortes con los ejes
\(f(x)=0\Rightarrow 2e^{x+1}=0\Rightarrow\hbox{Imposible}\) y \(f(0)=2e\), luego los cortes con los ejes serán \((0,2e)\)
– Para estudiar las asíntotas de la función consultar asíntotas y ver cómo resolver límites
. Asíntotas verticales: No hay ya que no hay puntos fuera del dominio de \(f(x)\)
. Asíntotas horizontales:
\(\lim\limits_{x\to\pm\infty}2e^{x+1}=+\infty\), luego no hay asíntotas verticales y tampoco oblicuas
– Los intervalos de crecimiento y decrecimiento se estudian calculando los máximos y mínimos de \(f(x)\), ver máximos y mínimos y la tabla de derivadas
\(f'(x)=2e^{x+1}=0\Rightarrow \hbox{Imposible porque}2e^{x+1}>0\), luego la función es siempre creciente
– Para estudiar la curvatura de la función se hallan los puntos de inflexión de \(f(x)\), ver cómo estudiar la curvatura de una función
\(f»(x)=2e^{x+1}=0\Rightarrow \hbox{Imposible porque}2e^{x+1}>0\), luego la función no cambia su curvatura
Así que la gráfica de la función será
2. Para hallar el área pedida y teniendo en cuenta la gráfica de la función \(f(x)\), ver funciones elementales, se evaluará la integral de la función entre \(0\) y \(1\), ver cómo se calcula una integral definida y consultar también la tabla de integrales
\(\displaystyle A=\int_0^{1}2e^{x+1}dx=2e^{x+1}\Big]_{0}^{1}=\bbox[yellow]{2e(e-1)}\)
\[\]Ejercicio 4: (2 ptos)
En la representación de navidad de los alumnos de 3º de primaria de un colegio hay tres tipos de papeles: 7 son de animales, 3 de personas y 12 de árboles. Los papeles se asignan al azar, los alumnos escogen por orden alfabético sobres cerrados en los que está escrito el papel que les ha correspondido
1. Calcúlese la probabilidad de que a los dos primeros alumnos les toque el mismo tipo de papel
2. Calcúlese la probabilidad de que el primer papel de persona le toque al tercer alumno de la lista
1. Recordar la teoría de probabilidad para hacer este ejercicio
Considerando:
\(A=\) Suceso de papel de animales
\(B=\) Suceso de papel de personas
\(C=\) Suceso de papel de árboles
Por el enunciado se sabe que \(P(A)=\frac{7}{22}, \;\; P(B)=\frac{3}{22},\;\; P(C)=\frac{12}{22}\)
Por lo tanto, la probabilidad de que a los dos primeros alumnos les toque el mismo papel será la probabilidad de que a ambos les toque un papel de animal más la probabilidad de que a ambos les toque de persona más la de que a ambos les toque de árbol, es decir;
\(P(\hbox{mismo papel})=P(AA)+P(BB)+P(CC)=\frac{7}{22}.\frac{6}{21}+\frac{3}{22}.\frac{2}{21}+\frac{12}{22}.\frac{11}{21}=\frac{30}{77}=\bbox[yellow]{0,38}\)
2. La probabilidad de que el primer papel de persona le toque al tercer alumno será la probabilidad de que le toque habiendo tocado al primero de animal y al segundo de árbol más la de que al primero le toque de árbol y al segundo de animal más la de que al primero y al segundo les toque de árbol más la de que al primero y al segundo les toque de animales, es decir,
\(P(\hbox{persona el tercer alumno})=P(ACB)+P(CAB)+P(CCB)+P(AAB)=\frac{7}{22}.\frac{12}{21}.\frac{3}{20}+\frac{12}{22}.\frac{7}{21}.\frac{3}{20}+\frac{12}{22}.\frac{11}{21}.\frac{3}{20}+\frac{7}{22}.\frac{6}{21}.\frac{3}{20}=\frac{171}{1540}=\bbox[yellow]{0,11}\)
\[\]Ejercicio 5: (2 ptos)
La estatura en centímetros (cm) de los varones mayores de edad de una determinada población se puede aproximar por una variable aleatoria con distribución normal de media \(\mu\) y desviación típica \(\sigma= 16\) cm.
1. Se tomó una muestra aleatoria simple de 625 individuos obteniéndose una media muestral \(x = 169\) cm. Hállese un intervalo de confianza al 98 % para \(\mu\).
2. ¿Cuál es el mínimo tamaño muestral necesario para que el error máximo cometido en la estimación de \(\mu\) por la media muestral sea menor que 4 cm, con un nivel de confianza del 90 %?
1. Para recordar la fórmula del intervalo de confianza revisar la teoría de estadística,
\(\hbox{IC}= (\bar{x}-z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt n}, \bar{x}+z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt n})\)
con \(\bar{x}=169\), \(\sigma=16\), \(n=625\) y \(z_{\frac{\alpha}{2}}=2,325\), por lo tanto,
\(\hbox{IC}= (169-2,325\frac{16}{\sqrt{625}}, 169+2,325\frac{16}{\sqrt{625}}=\bbox[yellow]{(167, 512; 170, 488)}\)
2. El error máximo viene dado por la siguiente expresión \(E=z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt n}\), ver teoría de estadística, por lo tanto se tiene
\(4=1,645\frac{16}{\sqrt n}\Rightarrow\bbox[yellow]{n=25}\)
Ir a la Opción B de este examen