Definición
Es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es constante
Ecuación general de la elipse (centrada en el origen \((0,0)\)): \(\bbox[yellow]{\frac{x^2}{a^2} + \frac{y^2}{b^2}=1}\)
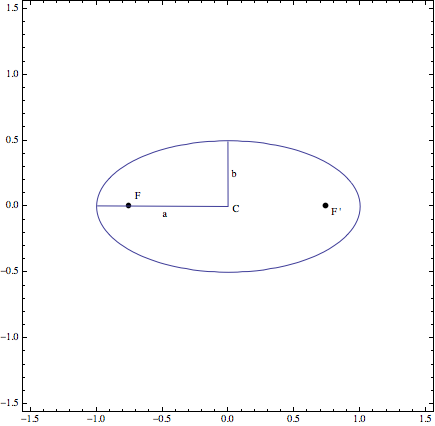
Centro: \(C\)
Semieje mayor: \(a\)
Semieje menor: \(b\)
Focos de la elipse: \(F\) y \(F’\)
Distancia focal: \(2c=\vec{FF’}\)
Ejemplo: Si \(F(-3,0)\) y \(F'(3,0)\Rightarrow 2c=6\)
Vértices: Los puntos que cortan al eje \(OX\) y al eje \(OY\)
Una elipse tiene \(4\) vértices, se calculan sustituyendo \(x=0\) e \(y=0\) en la ecuación general de la elipse
Excentricidad: \(e=\frac ca\)
Indica la forma de una elipse; una elipse será más redondeada cuanto más se aproxime su excentricidad al valor cero, si \(e=0\), se tratará de una circunferencia, ver geometría de la circunferencia
Expresión de \(a, b\) y \(c\): \(\bbox[yellow]{a^2=b^2+c^2}\)
Gráfica de una elipse
Volver a cónicas Ver ejercicios de cónicas