\[\] Ejercicio 6: Un trabajador en una inmobiliaria vende dos tipos de casas: pisos en las afueras, con los que gana \(1000\) euros por cada piso vendido y pisos en el centro, cuyos beneficios por piso vendido son de \(600\) euros para el trabajador. Por razones de mercado, la venta anual de las casas está sujeta a:
– El número de pisos en las afueras vendidos no será menor de \(50\) ni mayor de \(150\)
– El número de pisos en el centro vendidos ha de ser mayor o igual al de pisos en las afueras vendidos
– El trabajador puede vender hasta un máximo de \(500\) casas al año
1. Plantear las restricciones y representar gráficamente la región factible
2. ¿Cuántas casas de cada tipo debe vender anualmente el trabajador con el fin de maximizar los beneficios?
1. Primero se definen las variables a utilizar
\(x:\;\hbox{pisos en las afueras}\)
\(y:\;\hbox{pisos en el centro}\)
Las restricciones dadas por el enunciado pueden escribirse como un sistema de inecuaciones lineales, ver programación lineal,
\(\displaystyle\begin{cases}50\leq x\leq 150&\\x-y\leq 0&\\x+y\leq 500&\\\end{cases}\)
Resolviendo el sistema de inecuaciones, tomando dos a dos las ecuaciones, se obtendrán los vértices de la región buscada, ver cómo resolver problemas de programación lineal,
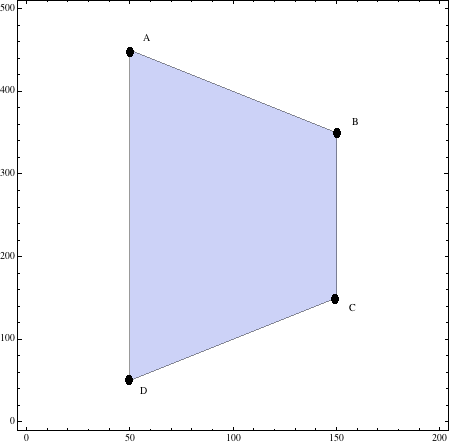
\(\bbox[yellow]{A(50,450),\;B(150,350),\;C(150,150)\;y\;D(50,50)}\)
Y la región será
2. La función objetivo en este caso será la función que se pide maximizar, es decir, las ventas de los tipos de casas, \(z(x,y)=1000x+600y\)
Evaluando la función en los vértices de la región se tiene
\(\displaystyle\begin{cases}z(50,50)=&8\\z(150,150)=&240000\\z(150,350)=&360000\\z(50,450)=&320000\\\end{cases}\)
De forma que para que el beneficio sea máximo \(\bbox[yellow]{\hbox{el trabajador tiene que vender }150\hbox{ pisos en las afueras y }350\hbox{ pisos en el centro}}\)
\[\] Ejercicio 7: Una agencia de viajes ofrece plazas para un hotel en el Caribe al precio de \(200\) euros y para familias con niños a un precio especial de \(90\) euros. A las familias con niños se les permite llevar \(80\) Kg de peso y al resto \(40\) Kg. Si el hotel dispone de \(90\) plazas y admite un equipaje de hasta \(3000\) Kg, ¿cuál debe ser la oferta de plazas de la agencia para optimizar el beneficio?
Nombrando en primer lugar las variables a utilizar, se tiene:
\(x:\;\hbox{plazas normales}\)
\(y:\;\hbox{plazas para familias}\)
Las restricciones dadas por el enunciado son
\(\displaystyle\begin{cases}x+y\leq&90\\40x+80y\leq&3000\\x,\;y\geq&0\\\end{cases}\Rightarrow\begin{cases}x+y\leq&90\\x+2y\leq&150\\x,\;y\geq&0\\\end{cases}\)
Resolviendo dos a dos el sistema de inecuaciones, se obtienen los vértices de la región buscada, ver cómo resolver problemas de programación lineal,
\(\bbox[yellow]{A(90,0),\;B(0,75),\;C(0,0)\;y\;D(30,60)}\)
Para dibujar la región se tendrán en cuenta estos vértices,
DIBU7
La función objetivo será \(z(x,y)=200x+90y\), ya que es la función que representa las ventas de ambas plazas. Sustituyendo los valores de los vértices \(A,\;B,\;C\;y\;D\) en la función \(z(x,y)\), se obtiene
\(\displaystyle\begin{cases}z(90,0)=&18000\\z(0,75)=&6750\\z(0,0)=&0\\z(30,60)=&11400\\\end{cases}\)
El máximo beneficio se obtiene ofertando \(\bbox[yellow]{ 90\hbox{ plazas generales en el hotel }}\)
\[\] Ejercicio 8: Calcular el valor máximo y el valor mínimo de la función \(z=10x+12y-35\) sujeta a las restricciones \(\displaystyle\begin{cases}x+y-2>&0\\2x+3y-4\leq&0\\x-y+5>&0\\\end{cases}\)
Para dibujar la región se resuelven las ecuaciones dadas en el enunciado dos a dos, hallando, de esta forma, los vértices de la región, ver programación lineal y cómo resolver sistemas de ecuaciones, obteniendo
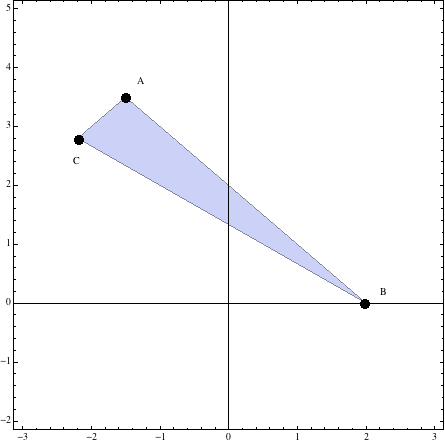
\(\bbox[yellow]{A(-\frac 32,\frac 72),\;B(2,0),\;y\;\;C(-\frac {11}5,\frac{14}5)}\)
Evaluando la función \(z(x,y)\) dada en los vértices obtenidos, ver programación lineal, se tiene
\(\displaystyle\begin{cases}z(2,0)=&-15\\z(-\frac 32,\frac 72)=&-8\\z(-\frac{11}5,\frac{14}5)=&-18,6\\\end{cases}\)
El valor máximo es \(\bbox[yellow]{ -8\hbox{ y corresponde al punto }(-\frac 32,\frac 72)}\)
El valor mínimo es \(\bbox[yellow]{ -18,6\hbox{ y corresponde al punto }(-\frac{11}5,\frac{14}5)}\)
\[\] Ejercicio 9: Se considera la función \(f(x,y)=x-y\)
Representar el conjunto
\(A=\{(x,y):3x+y\geq 15,\; y-x\leq -5,\; 2x+3y\leq 60,\; y\geq 0\}\)
y calcular el valor máximo de \(f(x,y)\) en \(A\)
Resolviendo el sistema de inecuaciones del conjunto \(A\) se obtienen los vértices de la región pedida, ver programación lineal,
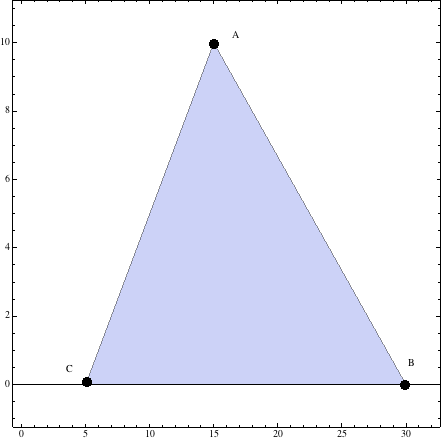
\(\bbox[yellow]{A(15,10),\;B(30,0),\;y\;\;C(5,0)}\) y la región pedida será
Evaluando la función \(z(x,y)\) dada en los vértices obtenidos, ver programación lineal, se tiene
\(\displaystyle\begin{cases}f(5,0)=&5\\f(30,0)=&30\\f(15,10)=&5\\\end{cases}\)
De manera que el valor máximo es \(\bbox[yellow]{ 30\hbox{ y corresponde al punto }(30,0)}\)
Ver ejercicios de Programación lineal en exámenes de acceso a la Universidad