Definiciones básicas
Grado– Medida de cada uno de los ángulos que resulta al dividir el ángulo recto en \(90\)º iguales. El grado tiene dos submúltiplos:
El minuto– Equivale a una sexagésima parte del grado- 1º=60′
El segundo– Equivale a la sexagésima parte del minuto- 1’=60»
Radián– Es el ángulo plano que teniendo su vértice en el centro de un círculo, intercepta sobre la circunferencia de ese círculo un arco de longitud igual al radio
La relación entre radianes y grados es
\(\bbox[yellow]{180 grados\equiv \pi radianes}\)
Trigonometría en triángulos
Pitágoras: Sea \(h\) la hipotenusa de un triángulo rectángulo y \(a\) y \(b\) sus catetos, entonces \(\bbox[yellow]{h^2=a^2+b^2}\)
La suma de todos los ángulos de un triángulo es \(180\) grados
\(\bbox[yellow]{\sin\alpha= \frac{a}{h}}\), con \(a\) el cateto opuesto al ángulo \(\alpha\)
\(\bbox[yellow]{\cos\alpha=\frac{b}{h}}\), con \(b\) el cateto contiguo al ángulo \(\alpha\)
Teorema del seno:
Sea \(A\) un vértice del triángulo y \(a\) el lado que está en frente de dicho vértice (el único lado no contiguo a \(A\))
Sea por otra parte \(B\) otro vértice y \(b\) el lado opuesto a dicho vértices, entonces se cumple:
\(\bbox[yellow]{\frac{b}{sen B}=\frac{a}{sen A}}\)
Sean \(a, b, c\) los lados de un triángulo y \(A\) el vértice enfrentado al lado \(a\), entonces: \(\bbox[yellow]{a^2=b^2+c^2-2.b.c.\cos A}\)
Definiciones de las funciones trigonométricas fundamentales
Función \(\sin x\)
Es una función continua y periódica, de período \(2\pi\), ver funciones continuas
El seno de un ángulo en un triángulo rectángulo se define como la razón entre el cateto opuesto y la hipotenusa, ver trigonometría en triángulos
| \(\sin 0=0\) | \(\sin \pi +k=0\) con \(k\in\mathbb{Z}\) |
|---|---|
| \(\sin \frac{\pi}{2}=1\) | \(\sin \frac{\pi}{2} +k=1\) con \(k\in\mathbb{Z}\) |
| \((\sin x)'=\cos x\) | \(\int\sin x dx=-\cos x +C\) |
| \(\sin (-x)=-\sin x\) | \(\sin ^{-1}x=\arcsin x\) |
Función \(\cos x\)
Es una función continua y periódica, de período \(2\pi\), ver funciones continuas
El coseno de un ángulo en un triángulo rectángulo se define como la razón entre el cateto contiguo y la hipotenusa, ver trigonometría en triángulos
| \(\cos 0=1\) | \(\cos \pi +k=1\) con \(k\in\mathbb{Z}\) |
|---|---|
| \(\cos \frac{\pi}{2}=0\) | \(\cos \frac{\pi}{2} +k=0\) con \(k\in\mathbb{Z}\) |
| \((\cos x)'=-\sin x\) | \(\int\cos x dx=\sin x+C\) |
| \(\cos (-x)=\cos x\) | \(\cos ^{-1}x=\arccos x\) |
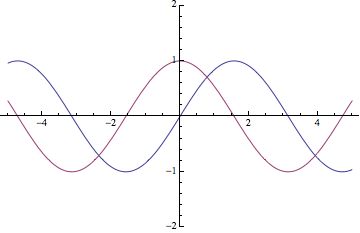
En la siguiente figura, la función \(\sin x\) está representada en azul y el \(\cos x\) en granate
Expresiones trigonométricas
| \(\sin^2 x+\cos^2 x=1\) | \(\tan ^2 x+1=\sec^2 x\) |
|---|---|
| \(\sec x=\frac{1}{\cos x}\) | \(\tan x=\frac{\sin x}{\cos x}\) |
| \(1+\cot ^2 x=\csc^2 x\) | \(\csc x=\frac{1}{\sin x}\) |
| \(\sin 2a=2\sin a.\cos b\) | \(\cos 2a= \cos^2a-\sin^2a\) |
|---|---|
| \(\sin (a+b)=\sin a.\sin b+\cos a.\cos b\) | \(\sin (a-b)=\sin a.\cos b-\cos a.\sin b\) |
| \(\cos(a+b)=\cos a.\cos b-\sin a.\sin b\) | \(\cos (a-b)=\cos a.\cos b+\sin a.\sin b\) |