Ejercicio :(Septiembre 2014 Opción B)(Calificación: 2 ptos)
Sea S la región del plano definida por \(y\geq 2x-4; y\leq x-1; 2y\geq x; x\geq 0; y\geq 0\)
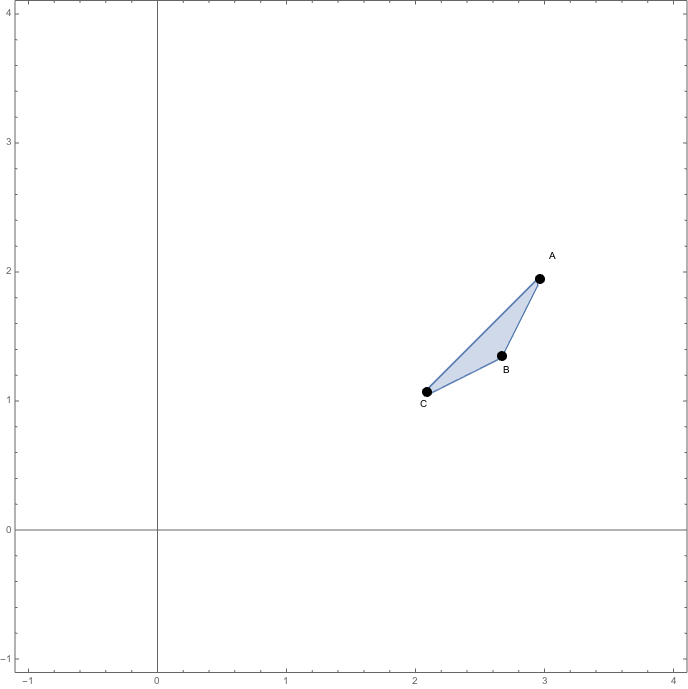
1. Represéntese la región \(S\) y calcúlese las coordenadas de sus vértices.
2. Obténgase los valores máximo y mínimo de la función \(f(x, y) = x−3y\) en \(S\) indicando los puntos de \(s\) en los cuales se alcanzan dichos valores máximo y mínimo
1. Para obtener los vértices de la región pedida, se resuelve el siguiente sistema de ecuaciones, ver cómo resolver problemas de programación lineal y consultando cómo resolver sistemas de ecuaciones se obtiene el resultado
\(\displaystyle\begin{cases}y=&2x-4\\y=&x-1\\\end{cases}\Rightarrow A(3,2)\)
\(\displaystyle\begin{cases}y=&2x-4\\2y=&x\\\end{cases}\Rightarrow B(\frac 83,\frac 43)\)
\(\displaystyle\begin{cases}y=&x-1\\x=&2y\\\end{cases}\Rightarrow C(2,1)\)
Y la región será
2. Los vértices de la región pedida se han calculado en el apartado anterior y son \(\bbox[yellow]{A(3,2),\;B(\frac 83,\frac 43),\;C(2,1)}\)
Sustituyendo los valores de los vértices de la región obtenida en la función objetivo \(f(x,y)\), se obtienen los siguientes resultados
\(\displaystyle\begin{cases}f(3,2)=&-1\\f(3,2)=&-3\\f(\frac 83,\frac 43)=&-\frac 43\\\end{cases}\)
Luego, \(f(x,y)\) alcanza el valor máximo en el punto \(\bbox[yellow]{C(2,1)\;\hbox{y vale }-1}\) y el mínimo en \(\bbox[yellow]{A(3,2)\;\hbox{y vale }-3}\)
Ejercicio : (Junio 2014 Opción A) (Calificación: 2 ptos)
Se considera la función \(f(x)=5x-2y\) y la región del plano \(S\) definida por el siguiente conjunto de restricciones:
\(x-2y\leq 0,\qquad\)\(x+y\leq 6,\qquad\)\(x\geq 0,\qquad\)\(y\leq 3\)
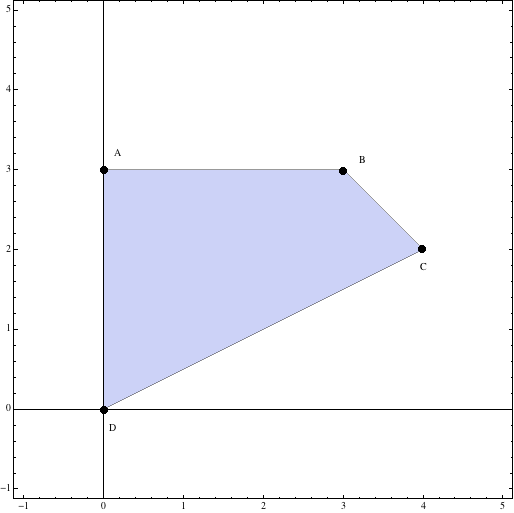
a) Represéntese la región \(S\)
b) Calcúlense las coordenadas de los vértices de la región \(S\) y obténgase los valores máximo y mínimo de la función \(f\) en \(S\) indicando los puntos donde se alcanzan
a) Para obtener los vértices de la región pedida, se resuelve el siguiente sistema de ecuaciones, ver cómo resolver problemas de programación lineal y consultando cómo resolver sistemas de ecuaciones se obtiene el resultado
\(\displaystyle\begin{cases}y=&3\\x=&0\\\end{cases}\Rightarrow A(0,3)\)
\(\displaystyle\begin{cases}x+y=&6\\y=&3\\\end{cases}\Rightarrow B(3,3)\)
\(\displaystyle\begin{cases}x+y=&6\\x-2y=&0\\\end{cases}\Rightarrow C(4,2)\)
\(\displaystyle\begin{cases}x-2y=&0\\x=&0\\\end{cases}\Rightarrow D(0,0)\)
Y la región será
b) Los vértices de la región pedida se han calculado en el apartado anterior y son \(\bbox[yellow]{A(0,3),\;B(3,3),\;C(4,2)\;y\;D(0,0)}\)
Sustituyendo los valores de los vértices de la región obtenida en la función objetivo \(f(x,y)\), se obtienen los siguientes resultados
\(\displaystyle\begin{cases}f(0,3)=&-6\\f(3,3)=&9\\f(4,2)=&16\\f(0,0)=&0\\\end{cases}\)
Luego, \(f(x,y)\) alcanza el valor máximo en el punto \(\bbox[yellow]{C(4,2)\;\hbox{y vale }16}\) y el mínimo en \(\bbox[yellow]{A(0,3)\;\hbox{y vale }-4}\)
Ver más ejercicios de Programación y Optimización en Selectividad