OPCIÓN B
\[\]Ejercicio 1:(2 ptos)
Considérese la matriz \(A=\begin{pmatrix}1 &0\\ 0& 0\\ 0& 1\end{pmatrix}.\)
a) Calcúlense \((A.A^{t})^{200}\)
b) Calcúlense \((A.A^{t}-3I)^{-1}\)
Nota: \(A^{-1}\) denota a la traspuesta de la matriz \(A\). \(I\) es la matriz identidad de orden 3
a) Consultando cómo multiplicar matrices, y cómo calcular la transpuesta de una matriz, se tiene
\(A.A^{t}=\begin{pmatrix}1 &0\\ 0& 0\\ 0& 1\end{pmatrix}.\begin{pmatrix}1 &0&0\\ 0& 0&1\end{pmatrix}=\begin{pmatrix}1 &0&0\\ 0& 0&0\\ 0& 0&1\end{pmatrix}\)
Y \((A.A^{t})^2=\begin{pmatrix}1 &0&0\\ 0& 0&0\\ 0& 0&1\end{pmatrix}.\begin{pmatrix}1 &0&0\\ 0& 0&0\\ 0& 0&1\end{pmatrix}=\begin{pmatrix}1 &0&0\\ 0& 0&0\\ 0& 0&1\end{pmatrix}\)
Por lo tanto, \(\bbox[yellow]{(A.A^{t})^{200}=\begin{pmatrix}1 &0&0\\ 0& 0&0\\ 0& 0&1\end{pmatrix}}\)
b) Recordando cómo restar matrices y teniendo en cuenta el apartado a), se obtiene
\(A.A^{t}-3I=\begin{pmatrix}1 &0&0\\ 0& 0&0\\ 0& 0&1\end{pmatrix}-3\begin{pmatrix}1 &0&0\\ 0& 1&0\\ 0& 0&1\end{pmatrix}=\begin{pmatrix}-2 &0&0\\ 0& -3&0\\ 0& 0&-2\end{pmatrix}\)
Consultando cómo calcular la inversa de una matriz se tiene el resultado:
\(\bbox[yellow]{(A.A^{t}-3I)^{-1}=\begin{pmatrix}-\frac 12 &0&0\\ 0& -\frac 13&0\\ 0& 0&-\frac 12\end{pmatrix}}\)
Ejercicio 2:(2 ptos)
Sea S la región del plano definida por \(y\geq 2x-4; y\leq x-1; 2y\geq x; x\geq 0; y\geq 0\)
1. Represéntese la región \(S\) y calcúlese las coordenadas de sus vértices.
2. Obténgase los valores máximo y mínimo de la función \(f(x, y) = x−3y\) en \(S\) indicando los puntos de \(s\) en los cuales se alcanzan dichos valores máximo y mínimo
1. Para obtener los vértices de la región pedida, se resuelve el siguiente sistema de ecuaciones, ver cómo resolver problemas de programación lineal y consultando cómo resolver sistemas de ecuaciones se obtiene el resultado
\(\displaystyle\begin{cases}y=&2x-4\\y=&x-1\\\end{cases}\Rightarrow A(3,2)\)
\(\displaystyle\begin{cases}y=&2x-4\\2y=&x\\\end{cases}\Rightarrow B(\frac 83,\frac 43)\)
\(\displaystyle\begin{cases}y=&x-1\\x=&2y\\\end{cases}\Rightarrow C(2,1)\)
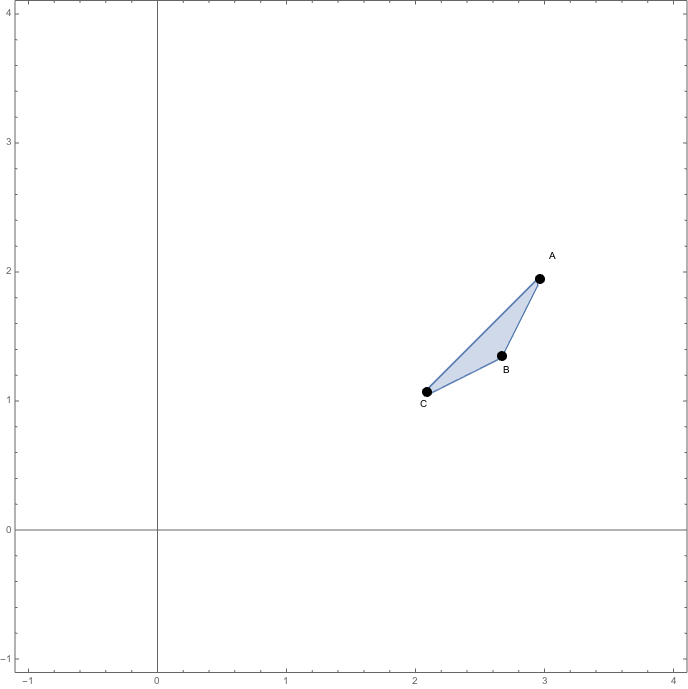
Y la región será
2. Los vértices de la región pedida se han calculado en el apartado anterior y son \(\bbox[yellow]{A(3,2),\;B(\frac 83,\frac 43),\;C(2,1)}\)
Sustituyendo los valores de los vértices de la región obtenida en la función objetivo \(f(x,y)\), se obtienen los siguientes resultados
\(\displaystyle\begin{cases}f(3,2)=&-1\\f(3,2)=&-3\\f(\frac 83,\frac 43)=&-\frac 43\\\end{cases}\)
Luego, \(f(x,y)\) alcanza el valor máximo en el punto \(\bbox[yellow]{C(2,1)\;\hbox{y vale }-1}\) y el mínimo en \(\bbox[yellow]{A(3,2)\;\hbox{y vale }-3}\)
\[\] Ejercicio 3:(2 ptos)
Se considera la función real de variable real definida por \(f(x)= \frac{\lambda x}{4+x^2}\)
1. Calcúlese el valor del parámetro real \(\lambda\) para que la recta tangente a la gráfica de f en \(x=-1\) sea paralela a la recta \(y=2x-3\)
2. Calcúlese \(\int_0^2 f(x)dx\) para \(\lambda = 1\)
1. Para que la recta tangente a \(f\) sea paralela a \(y=2x−3\) su pendiente tiene que ser la misma, ver condición rectas paralelas y ver también pendiente de una recta
\(f'(x)=\frac{\lambda(4-x^2)}{(x^2+4)^2}\) y se tiene que cumplir que \(f'(-1)=2\), por lo tanto, \(\lambda=\frac{50}{3}\)
2. Para calcular la integral pedida recordar la teoría sobre cálculo de integrales y la tabla de integrales,
\(\int_0^2 f(x)dx=\int_0^2 \frac{x}{4+x^2}dx=\frac 12\ln |4+x^2| \Big|_0^2=\bbox[yellow]{\frac{\ln 2}{2}}\)
\[\]Ejercicio 4:(2 ptos)
Al 80 % de los trabajadores en educación (E) que se jubilan sus compan ̃eros les hacen una fiesta de despedida (FD), también al 60% de los trabajadores de justicia (J) y al 30% de los de sanidad (S). En el último año se jubilaron el mismo número de trabajadores en educación que en sanidad, y el doble en educación que en justicia.
1. Calcúlese la probabilidad de que a un trabajador de estos sectores, que se jubiló, le hicieran una fiesta
2. Sabemos que a un trabajador jubilado elegido al azar de entre estos sectores, no le hicieron fiesta. Calcúlese la probabilidad de que fuera de sanidad
1. Recordando la teoría sobre probabilidades, se tiene que la probabilidad de que a un trabajador que se jubiló le hicieran una fiesta es la probabilidad de que dicho trabajadora fuera de educación, de justicia o de sanidad, es decir,
\(P(FD)=P(FD|E)P(E)+P(FD|J)P(J)+P(FD|S)P(S)=0,8.0, 4 + 0, 6 . 0, 4 + 0, 3 .0, 2 = \bbox[yellow]{0, 62}\)
2. La probabilidad pedida es una probabilidad condicionada, de manera que se calcula de la siguiente manera
\(P(S|noFD)= \frac{P(noFD|S)P(S)}{P(noFD)} = \frac{0,7.0,3}{1-0,62} =\bbox[yellow]{0,553}\)
\[\]Ejercicio 5:(2 ptos)
El mínimo tamaño muestral necesario para estimar la media de una determinada característica de una población que puede aproximarse por una variable aleatoria con distribución normal de desviación típica \(\sigma\), con un error máximo de 3,290 y un nivel de confianza del 90 %, supera en 7500 unidades al que se necesitaría si el nivel de confianza fuera del 95 % y el error máximo fuera de 7,840.
Exprésense los tamaños muestrales en función de la desviación típica \(\sigma\) y calcúlense la desviación típica de la población y los tamaños muestrales respectivos
Nota:Utilícese \(z_0,05 = 1, 645\)
Sabiendo la fórmula del error de estimación, se tiene que
\(E=z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}\)
Por lo tanto,
\(3,290=1,645\frac{\sigma}{\sqrt{n_1}}\Rightarrow \bbox[yellow]{n_1=0,25\sigma ^2}\)
y
\(7,840=1,96\frac{\sigma}{\sqrt{n_2}}\Rightarrow \bbox[yellow]{n_2=0,0625\sigma ^2}\)
Como el enunciado dice que el tamaño muestral \(n_1\) supera en 7500 al tamaño muestral \(n_2\), por lo tanto
\(n_1=n_2+7500\Rightarrow 0,25\sigma ^2= 0,0625\sigma ^2 + 7500\Rightarrow \bbox[yellow]{\sigma= 200}\)
Por lo tanto, \(n_1=0,25.(200)^2\) y \(n_2=0,0625.(200)^2\). Así que \(\bbox[yellow]{n_1=10000}\) y \(\bbox[yellow]{n_2=2500}\)