Ejercicio :(Septiembre 2010 Opción A) (Calificación: 3 ptos)
Es coste de un marco para una ventana rectangular es de \(50\) euros por cada metro de lado vertical y de \(25\) euros por cada metro de lado horizontal. Se desea construir una ventana de superficie igual a \(2m^2\). Calcúlese sus dimensiones (largo y alto) para que el marco sea lo más barato posible. Calcúlese el precio mínimo del marco de dicha ventana
Considerando \(x\) la longitud de la base del marco e \(y\) la altura, el coste (y la función a minimizar) será
\(P(x,y)=25.2x+50.2y=50x+100y\)
Teniendo en cuenta que el enunciado dice que el área es igual a \(2m^2\) y la fórmula para el área de un rectángulo, se tiene,
\(x.y=2\Rightarrow y=\frac 2x\)
Incluyendo este despeje en la ecuación a minimizar, se tiene
\(P(x)=50x+100\frac 2x=50x+\frac{200}{x}\)
Para hallar el mínimo pedido se deriva la función \(P(x)\) y se iguala a cero la derivada, ver cómo calcular máximos y mínimos de una función y consultar también la tabla de derivadas,
\(P'(x)=50-\frac{200}{x^2}=0\Rightarrow x=\pm 2\)
El valor negativo de \(x\) no tiene sentido (ya que se está hablando de la medida de un lado de un rectángulo), luego sólo se tendrá en cuenta \(x=2\)
Para comprobar si es mínimo el punto crítico obtenido se evalúa en la segunda derivada,
\(P»(x)=\frac{400}{x^3}\), luego, \(P»(2)=0\), de forma que \(x=2,y=\frac 22=1\) es un mínimo de la función \(P(x,y)\)
Por lo tanto, las dimensiones que hacen el coste mínimo son \(\bbox[yellow]{x=2m,y=1m}\)
El valor de este coste mínimo será \(P(2,1)=50.2+100.1\Rightarrow \bbox[yellow]{P(2,1)=200\hbox{ euros}}\)
Ejercicio : (Septiembre 2010 Opción B) (Calificación: 3 ptos)
Un pintor necesita pintura para pintar como mínimo una superficie de \(480m^2\). Puede comprar la pintura a dos proveedores, \(A\) y \(B\). El proveedor \(A\) le ofrece una pintura con un rendimiento de \(6m^2\) por Kg y un precio de \(1\) euro por Kg. La pintura del proveedor \(B\) tiene un precio de \(1,2\) euros por Kg y un rendimiento de \(8m^2\) por Kg. Ningún proveedor le puede suministrar más de \(75\) Kg de pintura y el presupuesto máximo del pintor es de \(120\) euros. Calcúlese la cantidad de pintura que el pintor tiene que comprar a cada proveedor para obtener el mínimo coste. Calcúlese dicho coste mínimo
Primeramente se identifican las variables del problema:
\(x\equiv\) Kg de pintura comprados al proveedor \(A\)
\(y\equiv\) Kg de pintura comprados al proveedor \(B\)
La función a maximizar será \(F(x,y)=1x+1,2y\)
Las restricciones obtenidas a partir del enunciado serán las siguientes:
\(6x+8y\geq 480,\quad\)\(\quad 0\leq x\leq 75,\quad\)\(\quad 0\leq y\leq 75,\quad\)\(\quad x+1,2y\leq 120,\quad\)\(\quad x\geq 0,\qquad y\geq 0\)
Para obtener los vértices de la región del enunciado, se resuelven las inecuaciones dos a dos, ver cómo resolver problemas de programación lineal y consultar cómo resolver sistemas de ecuaciones se obtiene el resultado
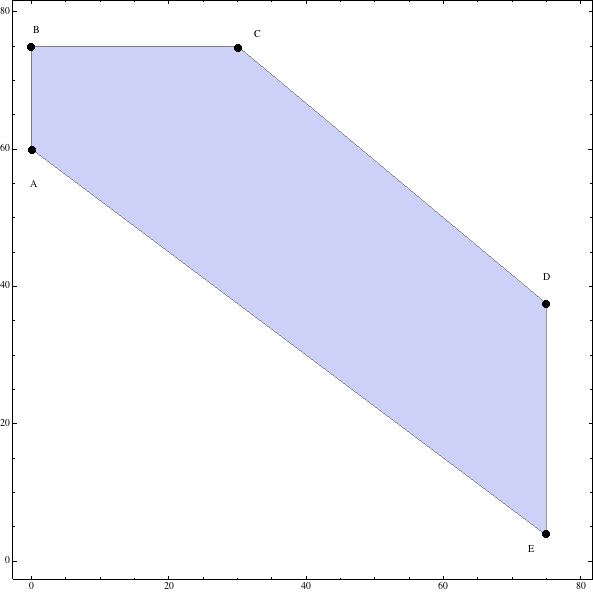
\(\displaystyle\begin{cases}x=&0\\6x+8y=&480\\\end{cases}\Rightarrow A(0,60)\)
\(\displaystyle\begin{cases}x=&0\\y=&75\\\end{cases}\Rightarrow B(0,75)\)
\(\displaystyle\begin{cases}x+1,2y=&120\\y=&75\\\end{cases}\Rightarrow C(30,75)\)
\(\displaystyle\begin{cases}x+1,2y=&120\\x=&75\\\end{cases}\Rightarrow D(75,37.5)\)
y
\(\displaystyle\begin{cases}x=&75\\6x+8y=&480\\\end{cases}\Rightarrow E(75, 3.75)\)
De forma que comprobando por ejemplo con el punto \((0,0)\) se dibuja la región será
Sustituyendo los valores de los vértices de la región obtenida en la función objetivo \(F(x,y)=x+1,2y\), se obtienen los siguientes resultados
\(\displaystyle\begin{cases}F(0,60)=&72\\F(0,75)=&90\\F(30,75)=&120\\F(75, 37.5)=&120\\F(75, 3.75)=&79,5\\\end{cases}\)
Luego, \(F(x,y)\) alcanza el valor mínimo en el punto \(A(0,60)\)
Por lo tanto, será necesario \(\bbox[yellow]{\hbox{ comprar }60\hbox{ kg de la pintura }B\hbox{ siendo el coste }72\hbox{ euros}}\)