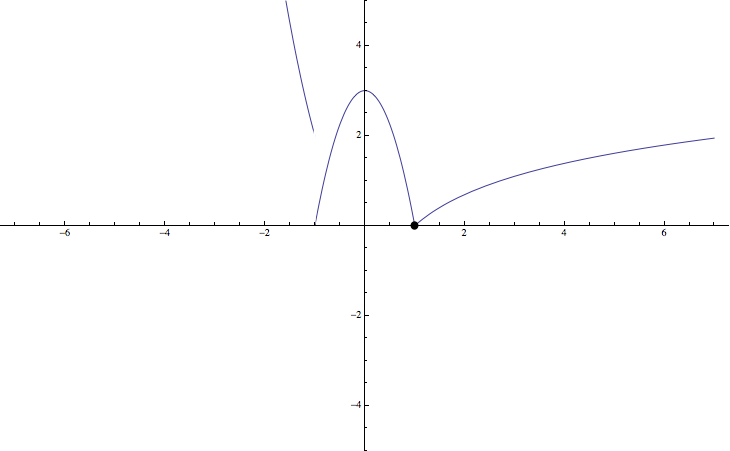
Ejercicio : (Junio 2010 Opción B) (Calificación: 3 ptos)
Dada la función: \(f(x)=\displaystyle\begin{cases}x+4&x<0\\ 4-x^2&0\leq x\leq 2\\ ax+b&x>2\\\end{cases}\)
a) (1 pto) Calcúlense \(a,b\) para que la función sea continua y derivable
b) (1 pto) Determínense la ecuación de la recta tangente a la gráfica de la función en el punto \(x=1\)
c) (1 pto) Para \(a=1,b=-2\), calcúlese el área de la región plana acotada limitada por la gráfica de la función y el eje \(OX\)
a) La función está formada por polinomios, luego el único punto de posible discontinuidad es el salto entre los polinomios, \(x=2\) (ver continuidad de funciones)
Para comprobar si la función es continua en dicho punto se evalúan los límites laterales y la función en el punto
\(\lim\limits_{x\to 2^{+}}f(x)=\lim\limits_{x\to 2^{+}}(ax+b)=2a+b\)
Calculando el otro límite lateral, se tiene
\(\lim\limits_{x\to 2^{-}}f(x)=\lim\limits_{x\to 2^{-}}(4-x^2)=4-2^2=0=f(2)\)
Luego, para que la función sea continua en \(2\) (y, por tanto, en todo \(\mathbb{R}\)), se debe cumplir que \(2a+b=0\)
Para que la función sea derivable tiene que cumplirse que \(f'(2^{-})=f'(2^{+})\), ver derivabilidad
En este caso, calculando primeramente la derivada de la función, ver la tabla de derivadas, se tiene
\(f'(x)=\displaystyle\begin{cases}1&x\leq 0\\ -2x&0\leq x\leq 2\\ a&x>2\\\end{cases}\)
Evaluando \(f'(2^{-})=f'(2^{+})\), se tiene que \(a=-4\), luego para que la función sea continua y derivable
\(\bbox[yellow]{a=-4,b=8}\)
b) La ecuación de la recta tangente en \(x=1\) viene dada por la siguiente ecuación, ver ecuaciones de la recta
\(y-f(1)=f'(1)(x-1)\)
Primeramente se calculará \(f(1)=4-1^2=3\) y la derivada de la función en el punto, \(f'(1)=-2\),
Por lo tanto, se tendrá el resultado \(y-3=-2(x-1)\Rightarrow\bbox[yellow]{y=-2x+5}\)
c) La función con \(a=1,b=-2\) será
\(f(x)=\displaystyle\begin{cases}x+4&x<0\\ 4-x^2&0\leq x\leq 2\\ x-2&x>2\\\end{cases}\)
Para hallar el área pedida, se calculará la integral definida de \(f(x)\), ver cómo se calcula una integral definida
Para saber los límites de la integral, se estudian los puntos de cortes de la función con el eje \(OX\),
\(x+4=0\Rightarrow x=-4\) y \(4-x^2=0\Rightarrow x=\pm 2\qquad\) y \(\qquad x-2=0\Rightarrow x=2\), como el valor \(x=-2\) no pertenece al intervalo del polinomio \(4-x^2\), no se considerará como límite de integración
De forma que los límites de la integral serán \(-4\) y \(0\) (ya que cero es el valor donde la función cambia al polinomio siguiente) para el polinomio \(x+4\) y \(0\) y \(2\) para \(4-x^2\), consultando la tabla de integrales es posible obtener el resultado pedido
\(A=\displaystyle\int_{-4}^0(x+4)dx+\displaystyle\int_{0}^2(4-x^2)dx=\frac{x^2}{2}+4x\Big]_{-4}^1+ 4x-\frac{x^3}{3}\Big]_0^2=8+8-\frac 83=\bbox[yellow]{\frac{40}{3}}\)
Ejercicio : (Septiembre 2010 Opción B) (Calificación: 3 ptos)
Dada la función: \(f(x)=\begin{cases}2x^2-a&x\leq -1\\ -3x^{2}+b & {-1}\leq x<1\\ \log x+a& x\geq 1\\\end{cases}\)
a) (1 pto) Calcúlense \(a,b\) para que la función sea continua en todos los puntos
b) (1 pto) Para \(a=0,b=3\), represéntese gráficamente la función
c) (1 pto) Para \(a=0,b=3\), calcúlese la integral definida \(\displaystyle\int_{-1}^1f(x)dx\)
a) La función está formada por tres polinomios, luego el único punto de posible discontinuidad es el salto entre estos tres polinomios, \(x=-1\) y \(x=1\) (ver continuidad de funciones)
Para comprobar si la función es continua en dichos puntos se evalúan los límites laterales y la función en los puntos
\(\lim\limits_{x\to -1^{+}}f(x)=\lim\limits_{x\to -1^{+}}(-3x^2+b)=-3(-1)^2+b=-3+b\)
Calculando el otro límite lateral y el valor de la función en el punto, queda
\(\lim\limits_{x\to -1^{-}}f(x)=\lim\limits_{x\to -1^{-}}(2x^2-a)=2-a=f(-1)\)
Luego, para que la función sea continua en \(-1\) se debe cumplir que \(2-a=-3+b\Rightarrow a+b=5\)
Por otra parte, en \(x=1\),
\(\lim\limits_{x\to 1^{+}}f(x)=\lim\limits_{x\to 1^{+}}(\log x+a)=\log 1+a=a=f(1)\)
Calculando el otro límite lateral y el valor de la función en el punto, queda
\(\lim\limits_{x\to 1^{-}}f(x)=\lim\limits_{x\to 1^{-}}(-3x^2+b)=-3.1^2+b=-3+b\)
Luego, para que la función sea continua en \(1\) (y, por tanto, en todo \(\mathbb{R}\)), se debe cumplir que \(a=-3+b\Rightarrow a-b=-3\)
Luego, para que la función sea continua en todos los puntos se tiene que cumplir \(a+b=5\hbox{ y }a-b=-3\Rightarrow\bbox[yellow]{a=1,b=4}\)
b) La función que se pide representar es
\(f(x)=\begin{cases}2x^2-a&x\leq -1\\ -3x^{2}+b & {-1}\leq x<1\\ \log x+a& x\geq 1\\\end{cases}\)
Para representar la función se seguirán los pasos para dibujar el gráfico de una función
– Como ya se ha comentado, el dominio en este caso serán todos los números reales, ver dominio de una función
– Para calcular el corte con los ejes se iguala la función a cero, ver cómo obtener los cortes con los ejes
\(f(x)=0\Rightarrow 2x^2=0,-3x^2+3=0,\log x=0\Rightarrow x=\pm 1, x=0\), como ni el cero ni el \(-1\) pertenecen a los intervalos en los cuales están los polinomios que anulan, se considerará únicamente el punto de corte \((1,0)\)
Por otra parte, al evaluar \(x=0\) en la función se tiene \(-3.0^2+3=3\), luego se obtiene el punto de corte, \((0,3)\)
Con estos datos y sabiendo que \(2x^2\) y \(-3x^2+3\) son parábolas y recordando la gráfica del logaritmo, ver funciones elementales, es posible dibujar la función
c) Al igual que en el apartado anterior, la función de la cual se pide el área es
\(f(x)=\displaystyle\begin{cases}2x^2&x\leq -1\\ -3x^2+3&-1<x<1\\ \log x+1&x\geq 1\\\end{cases}\)
Consultando la tabla de integrales y recordando cómo se resuelven integrales definidas, se tiene
\(\displaystyle\int_{-1}^1f(x)dx=\displaystyle\int_{-1}^1-3x^2+3dx=\frac{-3x^3}{3}+3x\Big]_{-1}^1=(1^3+3.1)-((-1)^3+3(-1))=4-(-4)=\bbox[yellow]{8}\)
Ver ejercicios de Programación lineal y optimización en Selectividad