Pasos para dibujar la gráfica de una función
Gráficas de funciones elementales
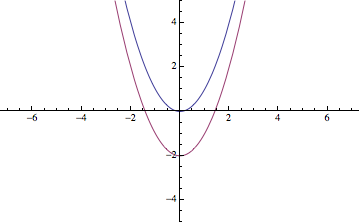
Parábola, \(y=x^2\)
Si se traslada la figura en el eje \(OX\), se tiene la expresión \(y=x^2\pm k\), y \(k\) será lo que suba o baje la parábola en el eje de las íes, ver geometría de una parábola
En la gráfica, la función azul es \(y=x^2\), y la roja es la trasladada \(y=x^2-2\)
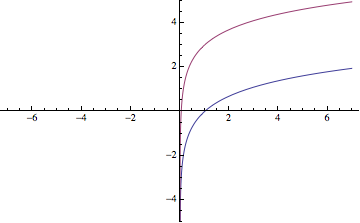
Logaritmo, \(y=\ln x\)
Si se traslada la figura, se tiene la expresión \(y=\ln x\pm k\), ver logaritmos
- Cuando la \(x\) se acerca al cero por la derecha, la función se va a menos infinito, \(\lim\limits_{x\to 0^{+}}\ln x=-\infty\)
- Cuando la \(x\) crece, la función crece, \(\lim\limits_{x\to\infty}\ln x=\infty\)
En la gráfica, la función azul es \(y=\ln x\), y la roja es la trasladada \(y=\ln x+3\)
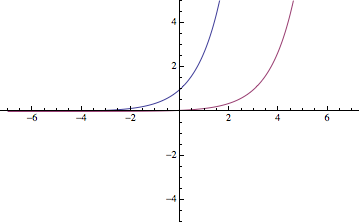
Exponencial, \(y=e^x\)
Es la función inversa de la función logaritmo neperiano, \(\ln x\). Si se traslada la figura se tiene la expresión \(y=e^{x\pm k}\)
- Cuando la \(x\) se acerca a menos infinito, la función tiene a \(0\), \(\lim\limits_{x\to -\infty}e^x=0\), ver cómo se resuelven límites
- Cuando la \(x\) crece, la función crece, \(\lim\limits_{x\to\infty}e^x=\infty\)
En la gráfica siguiente, la función azul es \(y=e^{x}\), y la roja es la trasladada \(y=e^{x-3}\)
Funciones trigonométricas
Algunas otras gráficas de funciones elementales pueden verse consultando las gráficas de funciones trigonométricas