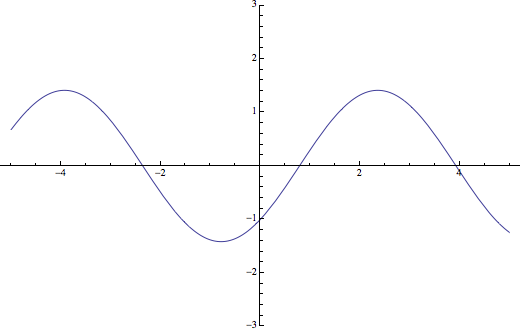
\[\]Ejercicio 1: Representar la función \(f(x)=\sin x-\cos x\)
Para representar la función se seguirán los pasos para dibujar el gráfico de una función
– El dominio de la función será todos los números reales, ver cómo calcular el dominio de una función
– Para calcular el corte con los ejes se iguala la función a cero, ver cómo obtener los cortes con los ejes
\(f(x)=0\Rightarrow \sin x=\cos x\), luego \(x=\frac{\pi}{4}+2k\pi\) y \(x=\frac{5\pi}{4}+2k\pi\) con \(k\in\mathbb{Z}\)
Por otra parte, como \(f(0)=-1\), la función pasará por \((0,-1)\)
– La función no tiene asíntotas, consultar asíntotas
– Los intervalos de crecimiento y decrecimiento se estudiarán calculando los máximos y mínimos de la función, ver máximos y mínimos y la tabla de derivadas
\(f'(x)=\cos x+\sin x=0\Rightarrow x=\frac{3\pi}{4}\) y \(\frac{7\pi}{4}\) en \([0,2\pi]\)
Para saber si los puntos críticos obtenidos son máximos o mínimos se evalúan en la segunda derivada,
\(f»(x)=-\sin x+\cos x\Rightarrow f»(\frac{3\pi}{4})=\frac{-2}{\sqrt{2}}<0\) y \(f»(\frac{7\pi}{4})=\frac{2}{\sqrt{2}}>0\)
Luego la función tiene un máximo en \((\frac{3\pi}{4},\frac{2}{\sqrt{2}})\) y un mínimo en \((\frac{7\pi}{4},\frac{-2}{\sqrt{2}})\)
Con los puntos estudiados es posible dibujar la función
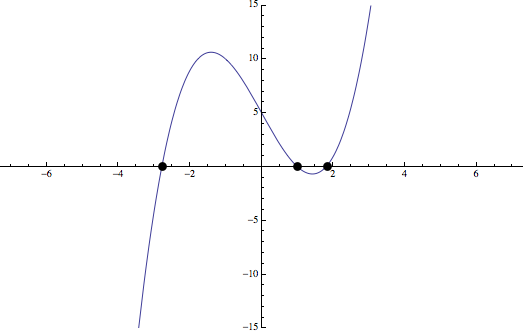
Ejercicio 2: Representar la función \(f(x)=x^3-6x+5\)
Para representar la función se van a seguirán los pasos para dibujar el gráfico de una función
Se trata de una función polinómica, ver representación de funciones elementales
– El dominio de dicha función serán todos los números reales, ver cómo calcular el dominio de una función
– Para calcular el corte con los ejes se iguala la función a cero y se iguala también \(x\) a cero, ver cómo obtener los cortes con los ejes y ver cómo se resuelven polinomios,
\(f(x)=0\Rightarrow x^3-6x+5=0\Rightarrow x=1,\). Haciendo la división de polinomios, se obtiene que \(x^3-6x+5=(x-1)(x^2+x-5)\)
Las soluciones de \(x^2+x-5\) son \(\frac{-1+\sqrt{21}}{2}\) y \(\frac{-1-\sqrt{21}}{2}\)
Los puntos de corte serán, por tanto: \((1,0)\), \((\frac{-1+\sqrt{21}}{2},0)\) y \((\frac{-1-\sqrt{21}}{2},0)\)
Por otra parte, \(f(0)=5\), luego la función también pasará por el punto \((0,5)\)
– Como es una función polinómica no tiene asíntotas, ver asíntotas
El comportamiento en el infinito será, ver cómo resolver límites,
\(\lim\limits_{x\to\infty}f(x)=\infty\)
– Los intervalos de crecimiento y decrecimiento se estudian calculando los máximos y mínimos de \(f(x)\), ver máximos y mínimos y la tabla de derivadas
\(f'(x)=3x^2-6=3(x^2-2)=0\Rightarrow x=\pm\sqrt{2}\)
Para comprobar si los puntos obtenidos son máximos o mínimos se estudia el signo de la primera derivada antes y después de los puntos críticos, en este caso, la función crece en \((-\infty,-\sqrt{2})\) y \((\sqrt{2},\infty)\) y decrece en \((-\sqrt{2},\sqrt{2})\)
De forma que tiene un máximo en \((-\sqrt{2},4\sqrt{2}+5)\) y un mínimo en \((\sqrt{2},5-4\sqrt{2})\)
– Para estudiar la curvatura de la función se hallan los puntos de inflexión de \(f(x)\), ver cómo estudiar la curvatura de una función
\(f»(x)=6x=0\Rightarrow x=0\), luego el punto de inflexión se encontrará en \((0,f(0)=5)\)
Estudiando el signo de la segunda derivada antes y después del cero se concluye que la función es cóncava en \((0,\infty)\) y convexa en \((-\infty,0)\)
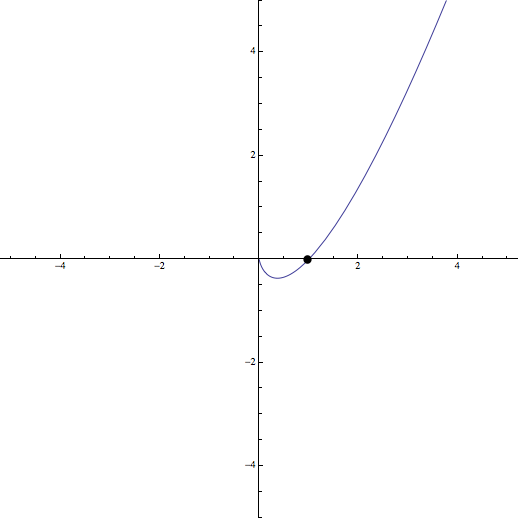
\[\] Ejercicio 3: Representar la función \(f(x)=x\ln x\)
Para representar la función se seguirán los pasos para dibujar el gráfico de una función
– El dominio de la función serán todos los números reales positivos, \((0,\infty)\), porque es el rango para el cual la función logaritmo tiene sentido, ver cómo calcular el dominio de una función
– Para calcular el corte con los ejes se iguala la función a cero y se iguala también \(x\) a cero, ver cómo obtener los cortes con los ejes y ver cómo se resuelven polinomios,
\(f(x)=0\Rightarrow x=1\) y \(x=0\). Como \(x=0\) no está en el dominio, el único punto de corte en este caso será \((1,0)\)
– La función no tiene asíntotas, ver asíntotas
– Los intervalos de crecimiento y decrecimiento se estudian calculando los máximos y mínimos de \(f(x)\), ver máximos y mínimos y la tabla de derivadas
\(f'(x)=\ln x +1=0\Rightarrow x=\frac{1}{e}\)
Para comprobar si el punto obtenido es máximo o mínimo se estudia el signo de la primera derivada antes y después de dicho punto, en este caso, la función decrece en \((0,\frac{1}{e})\) y crece en \((\frac{1}{e},\infty)\)
Luego, \((\frac{1}{e}, -0,37)\) es un mínimo de la función
– Para estudiar la curvatura de la función se hallan los puntos de inflexión de \(f(x)\), ver cómo estudiar la curvatura de una función
\(f»(x)=\frac 1x\Rightarrow \hbox{Imposible}\), luego no hay punto de inflexión
La segunda derivada \(\frac 1x\) es siempre positiva en el dominio de la función \((0,\infty)\), luego la función será cóncava en todo su dominio
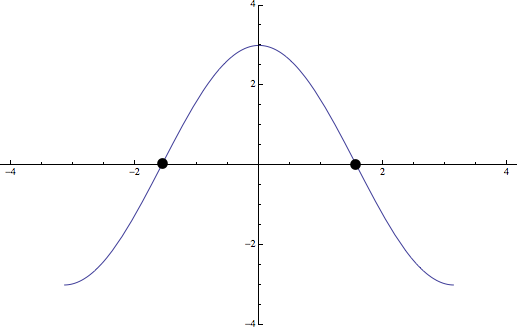
\[\]Ejercicio 4: Representar la función \(f(x)=3\cos x\) si \(x\in [-\pi,\pi]\)
La gráfica de la función es la gráfica de \(y=\cos x\) en \([-\pi,\pi]\) (ver ecuaciones trigonométricas) expandida con un factor de dilatación \(\frac 12\) en el eje \(OX\) y dilatada por un factor \(3\) en la dirección del eje \(OY\)
Ver más ejercicios de Representación de funciones