OPCIÓN B

\[\]Ejercicio 1: (3 ptos) Un estadio de fútbol con capacidad para \(72000\) espectadores está lleno durante la celebración de un partido entre los equipos \(A\) y \(B\). Unos espectadores son socios del equipo \(A\), otros lo son del equipo \(B\), y el resto no son socios de ninguno de los equipos. A través de la venta de localidades sabemos lo siguiente:

a) No hay espectadores que seam socios de ambos equipos simultáneamente
b) Por cada \(13\) socios de alguno de los dos equipos hay \(3\) espectadores que no son socios
c) Los socios del equipo \(B\) superan en \(6500\) a los socios del equipo \(A\)

¿Cuántos socios de cada equipo hay en el estadio viendo el partido?

Primeramente se escriben las variables que corresponden con los datos dados en el enunciado

\(x\equiv \hbox{n. socios de }A\)
\(y\equiv \hbox{n. socios de }B\)
\(z\equiv \hbox{n. socios de no socios}\)

De cada apartado del enunciado se puede deducir una ecuación:

\((a)\Rightarrow x+y+z=72000\)
\((b)\Rightarrow \frac{x+y}{13}=\frac z3\)
\((c)\Rightarrow y=6500+x\)

De forma que se tiene el siguiente sistema de ecuaciones

\(\begin{cases}x+y+z=72000&\\3x+3y-13z=0& \\x-y=-6500&\\\end{cases}\)

Resolviendo el sistema se tiene el resultado, ver cómo resolver un sistema de ecuaciones

\(\begin{cases}x+y+z=72000&\\3x+3y-13z=0& \\x-y=-6500&\\\end{cases}\Rightarrow x=26000,\;y=32500,\;z=13500\)

Por lo tanto, \(\bbox[yellow]{\hbox{hay }26000\hbox{ socios del equipo }A, 32500\hbox{ socios del equipo }B \hbox{ y }13500\hbox{ no socios }}\)

Ejercicio 2: (3 ptos) Dada la función: \(f(x)=\displaystyle\begin{cases}x^2-4x+3&x\leq 1\\ -x^2+4x-3&x>1\\\end{cases}\)

a) (1 pto) Estúdiese la continuidad y la derivabilidad de la función \(f(x)\)
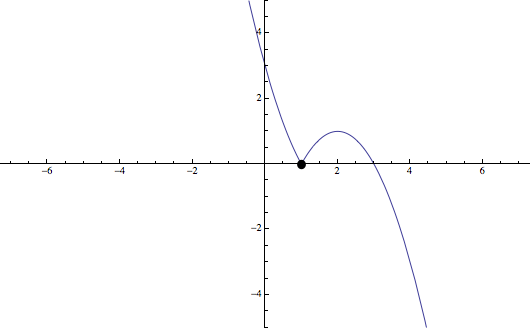
b) (1 pto) Represéntese gráficamente la función \(f(x)\)
c) (1 pto) Calcúlese el área del recinto plano acotado limitado por la gráfica de \(f(x)\), el eje \(OX\), el eje \(OY\) y la recta \(x=2\)

a) La función está formada por polinomios, luego el único punto de posible discontinuidad es el salto entre los polinomios, \(x=1\) (ver continuidad de funciones)

Para comprobar si la función es continua en dicho punto se evalúan los límites laterales y la función en el punto

\(\lim\limits_{x\to 1^{+}}f(x)=\lim\limits_{x\to 1^{+}}-x^2+4x-3=-1^2+4.1-3=0\)

Calculando el otro límite lateral, se tiene

\(\lim\limits_{x\to 1^{-}}f(x)=\lim\limits_{x\to 1^{-}}x^2-4x+3=0=f(1)\)

Luego, se cumple la condición de continuidad, luego \(\bbox[yellow]{f(x)\hbox{ es continua para todos los reales}}\)

Para que la función sea derivable tiene que cumplirse que \(f'(1^{-})=f'(1^{+})\), ver derivabilidad

En este caso, calculando primeramente la derivada de la función, se tiene

\(f'(x)=\displaystyle\begin{cases}2x-4&x\leq 1\\ -2x+4&x>1\\\end{cases}\)

Evaluando \(f'(1^{-})=f'(1^{+})\), se tiene que \(-2=2\Rightarrow \hbox{Imposible}\), luego, \(\bbox[yellow]{f(x) \hbox{ no es derivable en }x=1}\)

b) Para representar la función se seguirán los pasos para dibujar el gráfico de una función

– El dominio en este caso serán todos los números reales ya que está formada por dos polinomios, ver dominio de una función

– Para calcular el corte con los ejes se iguala la función a cero, ver cómo obtener los cortes con los ejes

\(f(x)=0\Rightarrow x^2-4x+3=0\) y \(-x^2+4x-3=0\), luego, consultando cómo resolver polinomios, se tienen las siguientes soluciones \(x=1\) y \(x=3\), luego la función cortará al eje \(OX\) en \((1,0)\) y en \((3,0)\) (ambos polinomios cortan al eje en esos puntos)

Por otra parte, evaluando \(f(0)\) se tiene \(f(0)=0^2-4.0+3=3\), luego otro punto de corte será \((0,3)\)

Con estos datos y sabiendo que ambos polinomios son parábolas trasladadas, recordar las funciones elementales es posible dibujar la función

c) Para hallar el área pedida y teniendo en cuenta la gráfica de la función \(f(x)\), los intervalos donde se define cada trozo de la función y la teoría de cómo se calcula una integral definida, se tiene

\(\displaystyle A=\int_0^{2}f(x)dx=\displaystyle\int_{0}^{1}(x^2-4x+3)dx+\int_1^2(-x^2+4x-3)dx=\frac{x^3}{3}-4\frac{x^2}{2}+3x\Big]_{0}^{1}-\frac{x^3}{3}+4\frac{x^2}{2}-3x\Big]_1^2=\frac 43-0+(-\frac 23)-(-\frac 43)=\bbox[yellow]{2}\)

\[\] Ejercicio 3: (2 ptos) Sean dos sucesos de un experimento aleatorio tales que:

\(P(A\cap B)=0,1\qquad\)\(\qquad P(\bar{A}\cap\bar{B})=0,6\qquad\)\(\qquad P(A|B)=0,5\qquad\)

Calcúlense
a) \(P(B)\)
b) \(P(A\cup B)\)
c) \(P(A)\)
d) \(P(\bar{B}|\bar{A})\)

a) Aplicando el Teorema de Bayes, ver probabilidad condicionada, se tiene

\(P(A|B)=\frac{P(A\cap B)}{P(B)}\Rightarrow P(B)=\frac{P(A\cap B)}{P(A|B)}=\frac{0,1}{0,5}=\bbox[yellow]{0,2}\)

b) Aplicando en este caso las leyes de Morgan, se tiene

\(P(\bar{A}\cap\bar{B})=P(\bar{A\cup B})=1-P(A\cup B)=1-P(\bar{A}\cap\bar{B})=1-0,6=\bbox[yellow]{0,4}\)

c) Con el dato obtenido en el apartado anterior se tiene el resultado en este caso

\(P(A\cup B)=P(A)+P(B)-P(A\cap B)\Rightarrow P(A)=P(A\cup B)+P(A\cap B)-P(B)=0,4+0,1-0,2=\bbox[yellow]{0,3}\)

d) Utilizando nuevamente el Teorema de Bayes, se tiene

\(P(\bar{B}|\bar{A})=\frac{P(\bar{B}\cap \bar{A})}{P(\bar{A})}=\frac{P(\bar{A}\cap \bar{B})}{1-P(A)}=\frac{0,6}{1-0,3}=\bbox[yellow]{0,8571}\)

\[\]Ejercicio 4: (2 ptos)Se supone que el gasto que hacen los individuos de una determinada población de regalos de Navidad se puede aproximar por una variable aleatoria con distribución normal de media \(\mu\) y desviación típica igual a \(45\) euros

a) Se toma una muestra aleatoria simple y se obtiene el intervalo de confianza \((251,6, 271,2)\) para \(\mu\), con un nivel de confianza del \(95\)%. calcúlese la media muestral y el tamaño de la muestra elegida

b) Se toma una muestra aleatoria simple de tamaño \(64\) para estimar \(\mu\). Calcúlese el error máximo cometido por esa estimación con un nivel de confianza del \(90\)%

a) Los intervalos de confianza están centrados en la media, ver intervalos de confianza en estadística, por lo tanto

\(\bar{x}=\frac{251,6+271,2}{2}=261,4\)

El tamaño muestral es posible obtenerlo a partir del error máximo permitido

\(E=\pm z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}\Rightarrow n=(z_{\frac{\alpha}{2}}\frac{\sigma}{E})^2\), ver teoría de estadística

En este caso, al ser \(95\)% el nivel de confianza, \(1-\alpha=0,95\Rightarrow\alpha=0,05\), y consultando la tabla de la normal, se tiene \(z_{\frac{\alpha}{2}}=1.96\), por lo tanto, \(n=(1,96\frac{45}{9,8})^2\Rightarrow\bbox[yellow]{n= 81}\)

b) El error máximo permitido viene dado por la fórmula

\(E=\pm z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}\), ver teoría de estadística

En este caso, al ser \(90\)% el nivel de confianza, \(1-\alpha=0,90\Rightarrow\alpha=0,10\), y consultando la tabla de la normal, se tiene \(z_{\frac{\alpha}{2}}=1.65\), por lo tanto, \(E=1,65\frac{45}{8}\Rightarrow\bbox[yellow]{n= 9,3}\)