OPCIÓN A
\[\]Ejercicio 1: (3 ptos) Un pintor dispone de dos tipos de pintura para realizar su trabajo. El primer tipo de pintura tiene un rendimiento de \(3m^2\) por litro, con un coste de \(1\) euros por litro. El segundo tipo de pintura tiene un rendimiento de \(4m^2\) por litro, con un coste de \(1,2\) euros por litro. Con ambos tipos de pintura se puede pintar a un ritmo de \(1\) litro cada \(10\) minutos. El pintor dispone de un presupuesto de \(480\) euros y no puede pintar durante más de \(75\) horas. Además, debe utilizar al menos \(120\) litros de cada tipo de pintura. Determínese la cantidad de pintura que debe utilizar de cada tipo si su objetivo es pintar la máxima superficie posible. Indíquese cuál es la superficie máxima
Primeramente se identifican las variables del problema:
\(x\equiv\) Litros de pintura del primer tipo
\(y\equiv\) Litros de pintura del segundo tipo
La función a maximizar será \(F(x,y)=3x+4y\)
Las restricciones obtenidas a partir del enunciado serán las siguientes:
\(10x+10y\leq 75.60\Rightarrow x+y\leq 450\)
\(1x+1,2y\leq 480\Rightarrow 5x+6y\leq 2400\)
\(x\geq 120,\qquad y\geq 120\)
Para obtener los vértices de la región pedida, se resuelven las inecuaciones dos a dos, ver cómo resolver problemas de programación lineal y consultar cómo resolver sistemas de ecuaciones se obtiene el resultado
\(\displaystyle\begin{cases}x=&120\\y=&120\\\end{cases}\Rightarrow A(120,120)\)
\(\displaystyle\begin{cases}x+y=&450\\y=&120\\\end{cases}\Rightarrow B(330,120)\)
\(\displaystyle\begin{cases}x+y=&450\\5x+6y=&2400\\\end{cases}\Rightarrow C(300,150)\)
y
\(\displaystyle\begin{cases}x=&120\\5x+6y=&2400\\\end{cases}\Rightarrow D(120,300)\)
De forma que los vértices de la región del enunciado serán
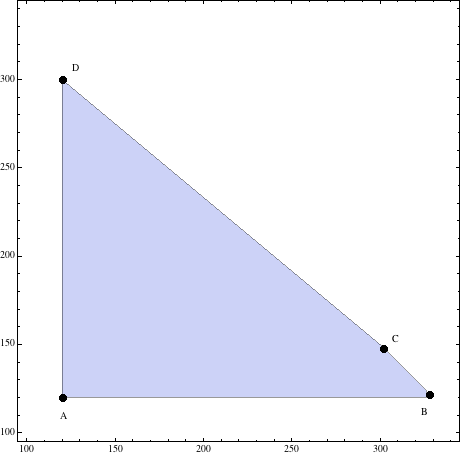
\(\bbox[yellow]{A(120,120),\;B(330,120),\;C(300,150)\;y\;D(120,300)}\)
Y la región será
Sustituyendo los valores de los vértices de la región obtenida en la función objetivo \(F(x,y)=3x+4y\), se obtienen los siguientes resultados
\(\displaystyle\begin{cases}F(120,120)=&840\\F(330,120)=&1470\\F(300,150)=&1500\\F(120,300)=&1560\\\end{cases}\)
Luego, \(F(x,y)\) alcanza el valor máximo en el punto \(D(120,300)\)
Por lo tanto, serán necesarios \(\bbox[yellow]{120\hbox{ litros de pintura del primer tipo y }300\hbox{ litros del segundo tipo}}\)
Ejercicio 2: (3 ptos) Se considera la función real de variable real definida por \(f(x)=\frac{x(2x-1)}{x-1}\)
a) (1 pto) Determínense las asíntotas de \(f(x)\). Calcúlense los extremos relativos de \(f(x)\)
b) (1 pto) Represéntese gráficamente la funcón \(f(x)\)
c) (1 pto) Calcúlese \(\displaystyle\int_2^5\frac{f(x)}{x^2}dx\)
a) Para estudiar las asintótas de la función, consultar el apartado de teoría de asíntotas
. Asintótas verticales:
Las posibles asíntotas verticales estarían en los puntos que no están en el dominio, ver cómo se calcula el dominio de una función. En este caso, el denominador se anula en \(x=1\), consultando cómo resolver límites, se tiene
\(\lim\limits_{x\to 1^{-}}\frac{x(2x-1)}{x-1}=-\infty\)
\(\lim\limits_{x\to 1^{+}}\frac{x(2x-1)}{x-1}=\infty\)
Luego, hay una asíntota vertical en \(\bbox[yellow]{x=1}\)
. Asintótas horizontales:
Consultando cómo se resuelven límites, se tiene que
\(\lim\limits_{x\to\pm\infty}\frac{x(2x-1)}{x-1}=\frac{\pm\infty}{\pm\infty}\)
Se obtiene una indeterminación (ver indeterminaciones), para resolver el límite (ver cómo resolver límites), se utiliza la Regla de L’Hôpital (ver la Regla de L’Hôpital y la tabla de derivadas),
\(\lim\limits_{x\to\pm\infty}\frac{x(2x-1)}{x-1}=\lim\limits_{x\to\pm\infty}4x=\pm\infty\)
Luego, \(\bbox[yellow]{\hbox{no hay horizontales}}\)
. Asintótas oblicuas:
Las posibles asíntotas oblicuas tendrían la siguiente expresión \(y=mx+n\)
Con \(m=\lim\limits_{x\to\pm\infty}\frac{f(x)}{x}\), usando de nuevo
la Regla de L’Hôpital, se tiene
\(m=\lim\limits_{x\to\pm\infty}\frac{\frac{2x^2-x}{x-1}}{x}=\lim\limits_{x\to\pm\infty}\frac{2x^2-x}{x^2-x}=2\)
Y \(n=\lim\limits_{x\to\pm\infty}(f(x)-mx)=\lim\limits_{x\to\pm\infty}(\frac{2x^2-x}{x-1}-2x)=\lim\limits_{x\to\pm\infty}\frac{x}{x-1}=1\)
Luego, la recta \(\bbox[yellow]{y=2x+1}\) será asíntota oblicua
Los extremos relativos (máximos y mínimos) se estudiarán derivando la función e igualándola a cero, ver máximos y mínimos, la tabla de derivadas y consultar también cómo resolver polinomios
\(f'(x)=\frac{(4x-1)(x-1)-(2x^2-x).1}{(x-1)^2}=0\Rightarrow 2x^2-4x+1=0\Rightarrow x=1\pm\frac{\sqrt{2}}{2}\)
Para saber si los puntos críticos obtenidos son máximos o mínimos, se evalúan en la segunda derivada,
\(f»(x)=\frac{(4x-4)(x-1)-2(2x^2-4x+1)}{(x-1)^3}=\frac{2}{(x-1)^3}\)
Sustituyendo los valores obtenidos, \(x=1\pm\frac{\sqrt{2}}{2}\), se tiene que
\(f»(1-\frac{\sqrt{2}}{2})=\frac{2}{(1+\frac{\sqrt{2}}{2}-1)^3}=4\sqrt{2}>0\qquad\) y \(\qquad f»(1+\frac{\sqrt{2}}{2})=\frac{2}{(1-\frac{\sqrt{2}}{2}-1)^3}=-4\sqrt{2}<0\)
De esta forma, consultando cómo saber si los puntos críticos son máximos o mínimos, se concluye que (sabiendo que \(f(1\pm\frac{\sqrt{2}}{2})=3\pm2\sqrt{2}\)) la función tiene
\(\bbox[yellow]{\hbox{min. en }(1+\frac{\sqrt{2}}{2},3+2\sqrt{2})}\) y \(\bbox[yellow]{\hbox{max. en }(1-\frac{\sqrt{2}}{2},3-2\sqrt{2})}\)
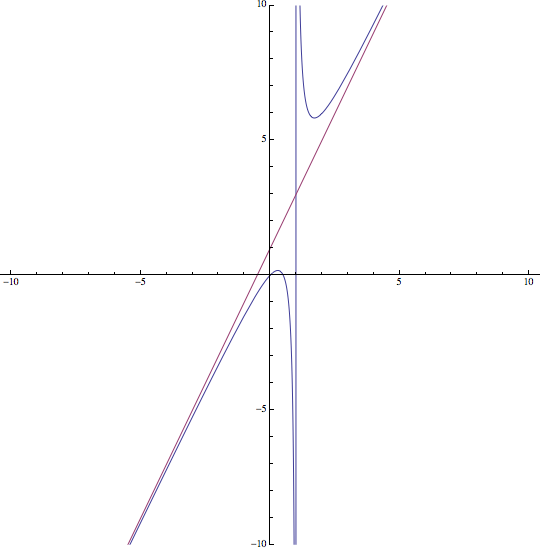
b) Para representar la función se seguirán los pasos para dibujar el gráfico de una función
– El dominio en este caso serán todos los números reales menos el \(\{1\}\) ya que el denominador se anula en ese valor, ver dominio de una función
– Para calcular el corte con los ejes se iguala la función a cero, ver cómo obtener los cortes con los ejes
\(f(x)=0\Rightarrow 2x^2-x=0\Rightarrow x=0\) y \(x=\frac 12\), luego se tienen los puntos de corte \((0,0)\) y \((\frac 12,0)\)
Por otra parte, evaluando \(f(0)\) se tiene \(f(0)=0\), luego se obtiene el mismo punto de corte hallado antes, \((0,0)\)
Con estos datos y los obtenidos en el apartado anterior, es posible dibujar la función
c) Consultando la tabla de integrales y recordando cómo se resuelven integrales definidas y teniendo en cuenta algunas propiedades de los logaritmos, se tiene
\(\displaystyle\int_2^5\frac{f(x)}{x^2}dx=\displaystyle\int_2^5 \frac{\frac{x(2x-1)}{x-1}}{x^2}dx=\displaystyle\int_2^5 \frac{2x-1}{x^2-x}dx=\ln |x^2-x|\Big]_2^5=\ln 20-\ln 2=\ln\frac{20}{2}=\bbox[yellow]{\ln 10}\)
\[\]Ejercicio 4: (2 ptos) Se dispone de cinco cajas opacas. Una contiene una bola blanca, dos contienen una bola negra y las otras dos están vacías. Un juego consiste en ir seleccionando al azar y secuencialmente una caja no seleccionada previamente hasta obtener una que contenga una bola. Si la bola de la caja seleccionada es blanca, el jugador ganar; si es negra, el jugador pierde
a) Calcúlese la probabilidad de que el jugador gane
b) Si el jugador ha perdido, ¿cuál es la probabilidad de que haya seleccionado una sóla caja?
a) Para resolver el problema se definen primeramente las variables a utilizar:
\(B\equiv\) Bola blanca
\(N\equiv\) Bola negra
\(V\equiv\) Urna vacía
\(G\equiv\) Ganar el juego
Los datos que da el enunciado son los siguientes
\(P(B)=\frac{1}{5}\)
\(P(N)=\frac{2}{5}\)
\(P(V)=\frac 25\)
\(P(B|V)=\frac 14\)
\(P(V|V)=\frac 14\)
\(P(B|V\cap V)=\frac 13\)
a) La probabilidad de ganar será la probabilidad de ganar habiendo sacado la bola blanca de la primera caja, más la probabilidad de que la primera caja estuviera vacía y haber sacado la bola blanca en la segunda caja y más la probabilidad de que las dos primeras cajas escogidas estuvieran vacías y haber sacado la bola blanca finalmente de la tercera caja, ver la teoría de la probabilidad
\(P(G)=P(B\cup(V\cap B)\cup (V\cap\cap V \cap B))=P(B)+P(V\cap B)+P(V\cap V\cap B)=P(B)+P(V).P(V|V).P(B|V\cap V)=\frac 15+\frac 25.\frac 14+\frac 25.\frac 14.\frac 13=\bbox[yellow]{\frac 13}\)
b) La probabilidad de que el jugador haya seleccionado una sóla caja sabiendo que ha ganado el juego será una probabilidad condicionada,
probabilidad condicionada
\(P(N|\bar{G})=\frac{P(N\cap \bar{G})}{P(\bar{G})}=\frac{P(N)}{1-P(G)}=\frac{\frac 25}{1-\frac 13}=\bbox[yellow]{\frac 35}\)
\[\]Ejercicio 4: (2 ptos) La duración en kilómetros de los neumáticos de una cierta marca se puede aproximar por una variable aleatoria con distribución normal de media \(\mu\) desconocida y desviación típica igual a \(3000\) kilómetros
a) Se toma una muestra aleatoria simple de \(100\) neumáticos y se obtiene una media muestral de \(48000\) kilómetros. Determínese un intervalo de confianza con un nivel del \(90\)% para \(\mu\)
b) Calcúlese el tamaño mínimo que debe tener la muestra para que el valor absoluto de la diferencia entre la media de la muestra y \(\mu\) sea menor o igual a \(1000\) kilómetros con probabilidad mayor o igual que \(0,95\)
a) Llamando \(x\) a la variable aleatoria que mida la duración en Km de los neumáticos, se tendría que dicha variable se comporta como una normal \(x:N(\mu,\sigma)\)
Para muestras de tamaño \(100\), las medias también siguen una distribución Normal, \(\bar{x}:N(\mu,\frac{3000}{\sqrt{100}})\)
Para una muestra de este tamaño, se ha obtenido una media muestral de \(\bar{x}=48000\)
El intervalo de confianza se hallará con la siguiente fórmula, ver teoría de estadística,
\(IC=(\bar{x}-z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}},\bar{x}+z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}})\)
El valor de \(z_{\frac{\alpha}{2}}\) se obtiene a partir del nivel de confianza dado en el enunciado y consultando la tabla de la normal
Nivel de confianza del \(90\hbox{%}\Rightarrow 1-\alpha=0,90\Rightarrow \alpha=0,1\Rightarrow z_{\frac{\alpha}{2}}=1,645\)
Por lo tanto,
\(IC=(48000-1,645\frac{3000}{\sqrt{100}},48000+1,645\frac{3000}{\sqrt{100}})=\bbox[yellow]{(47505, 48495)}\)
b) El tamaño muestral es posible obtenerlo a partir del error máximo permitido
\(E=\pm z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}\Rightarrow n=(z_{\frac{\alpha}{2}}\frac{\sigma}{E})^2\), ver teoría de estadística
En este caso, al ser \(95\)% el nivel de confianza, \(1-\alpha=0,95\Rightarrow\alpha=0,05\), y consultando la tabla de la normal, se tiene \(z_{\frac{\alpha}{2}}=1.96\), por lo tanto, \(n>(1,96\frac{3000}{1000})^2=34,6\Rightarrow\bbox[yellow]{n\geq 35}\)
Ir a la Opción B de este examen