OPCIÓN A
\[\]Ejercicio 1: (3 ptos) Se considera la región \(S\) acotada plana definida por las cinco condiciones siguientes:
\(x+y\leq 4,\qquad\)\(x-y\leq 4,\qquad\)\(2x-3y\geq -6,\qquad\)\(2x+3y\geq -6,\qquad\)\(x\leq 2\)
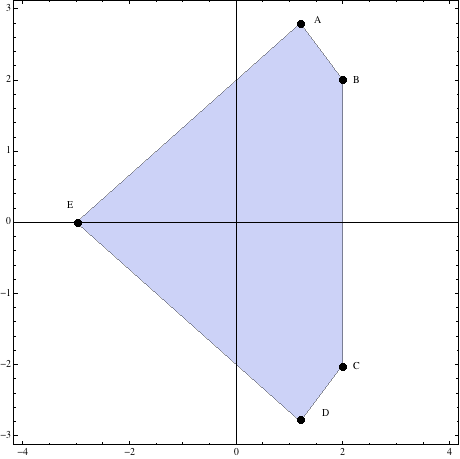
a) Dibújese \(S\) y calcúlense las coordenadas de sus vértices
b) Calcúlense los valores máximo y mínimo de la función \(f(x,y)=2x+y\) en la región \(S\) y especifíquense los puntos de \(S\) en los cuales se alcanzan dichos valores máximo y mínimo
a) Para obtener los vértices de la región pedida, se resuelven las ecuaciones de dos en dos, ver cómo resolver problemas de programación lineal y consultar cómo resolver sistemas de ecuaciones se obtiene el resultado
\(\displaystyle\begin{cases}x+y=&4\\2x-3y=&-6\\\end{cases}\Rightarrow A(\frac 65,\frac{14}{5})\)
\(\displaystyle\begin{cases}x+y=&4\\x=&2\\\end{cases}\Rightarrow B(2,2)\)
\(\displaystyle\begin{cases}x-y=&4\\x=&2\\\end{cases}\Rightarrow C(2,-2)\)
\(\displaystyle\begin{cases}x-y=&4\\2x+3y=&-6\\\end{cases}\Rightarrow D(\frac 65,-\frac{14}{5})\)
y
\(\displaystyle\begin{cases}2x+3y=&-6\\2x-3y=&-6\\\end{cases}\Rightarrow E(-3,0)\)
Con los vértices obtenidos, se puede dibujar la región pedida
b) Sustituyendo los valores de los vértices de la región obtenida en la función objetiva \(f(x,y)=2x+y\), se obtienen los siguientes resultados
\(\displaystyle\begin{cases}f(\frac 65,\frac{14}{5})=&\frac{26}{5}\\f(2,2)=&6\\f(2,-2)=&2\\f(\frac 65,-\frac{14}{5})=&-\frac 25\\f(-3,0)=&-6\\\end{cases}\)
Luego, \(f(x,y)\) alcanza: \(\bbox[yellow]{\hbox{un max. en }B(2,2)\;\hbox{con valor }6}\quad\) y \(\quad\bbox[yellow]{\hbox{un min. en }E(-3,0)\;\hbox{con valor }-6}\)
Ejercicio 2: (3 ptos) Dada la función \(f(x)=\frac{(x+1)^2}{x^2+1}\)
se pide:
a) (1 pto) Determínense las asíntotas de \(f(x)\). Calcúlense los extremos relativos de \(f\)
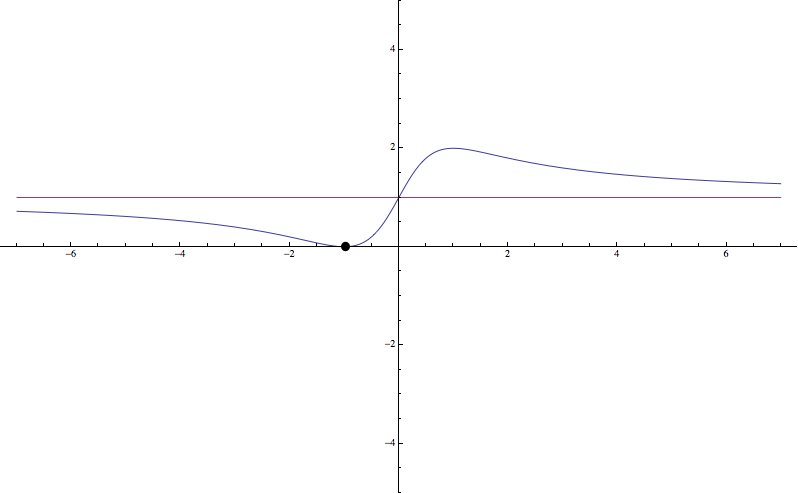
b) (1 pto) Represéntese gráficamente la función \(f(x)\)
c) (1 pto) Calcúlese el área del recinto acotado plano que limitan la gráfica de \(f(x)\), la recta horizontal \(y=1\) y la recta vertical \(x=1\)
a) Para estudiar las asintótas de la función, consultar el apartado de teoría de asíntotas
. Asintótas verticales:
Las posibles asíntotas verticales estarían en los puntos que no están en el dominio, ver cómo se calcula el dominio de una función. En este caso, el denominador no se anula en ningún valor real, \(x^2+1=0\Rightarrow x=\sqrt{-1}\), \(\bbox[yellow]{\hbox{no hay verticales}}\)
. Asintótas horizontales:
Consultando cómo se resuelven límites y utilizando la Regla de L’Hôpital se tiene que
\(\lim\limits_{x\to\infty}\frac{(x+1)^2}{x^2+1}=1\)
Luego, hay una asíntota horizontal en \(\bbox[yellow]{\hbox{horizontales }\equiv y=1}\)
. Asintótas oblicuas:
Como hay asíntotas horizontales, \(\bbox[yellow]{\hbox{no hay oblicuas}}\), ver la teoría de asíntotas
Los extremos relativos de la función (máximos y mínimos) se calcularán igualando la derivada de la función a cero, ver máximos y mínimos y la tabla de derivadas
\(f'(x)=\frac{2(x+1).1.(x^2+1)-(x+1)^22x}{(x^2+1)^2}=0\Rightarrow \frac{2(x+1)(1-x)}{(x^2+1)^2}=0\Rightarrow \frac{2(1-x^2)}{(x^2+1)^2}=0\Rightarrow x=\pm 1\)
Para saber si los puntos críticos obtenidos son máximos o mínimos, se evalúan en la segunda derivada,
\(f»(x)=2\frac{-2x(x^2+1)^2-(1-x^2)2(x^2+1)2x}{(x^2+1)^4}=\frac{4x(x^2-3)}{(x^2+1)^3}\)
Sustituyendo los valores obtenidos, \(x=\pm 1\), se tiene que \(f»(-1)=1>0\) y \(f»(1)=-1<0\)
De esta forma, consultando cómo saber si los puntos críticos son máximos o mínimos, se concluye que (sabiendo que \(f(-1)=0\hbox{ y } f(1)=2\)) la función tiene \(\bbox[yellow]{\hbox{min. en }(-1,0)}\) y \(\bbox[yellow]{\hbox{max. en }(1,2)}\)
b) Para representar la función se seguirán los pasos para dibujar el gráfico de una función
– Como ya se ha comentado, el dominio en este caso serán todos los números reales ya que el denominador no se anula para ningún valor real
– Para calcular el corte con los ejes se iguala la función a cero, ver cómo obtener los cortes con los ejes
\(f(x)=0\Rightarrow x=-1\), luego la función pasará por \((-1,0)\)
Por otra parte, como \(f(0)=1\), se obtiene el punto de corte, \((0,1)\)
Con estos datos y los obtenidos en los apartados anteriores, es posible dibujar la función
c) Para hallar el área pedida, se calculará la integral definida de la resta entre \(f(x)\) y \(y=1\), ver cómo se calcula una integral definida
\(A=\displaystyle\int_0^1\frac{(x^2+1)^2}{x^2+1}-1dx=\int_0^1\frac{2x}{x^2+1}dx=\ln (x^2+1)\Big]_0^1=\ln (1^2+1)-\ln (0^2+1)=\bbox[yellow]{\ln 2}\)
\[\] Ejercicio 3: (2 ptos) Se supone que la probabilidad de que nazca una niña es \(0,49\) y la probabilidad de que nazca niño es \(0,51\). Una familia tiene dos hijos
a) ¿Cuál es la probabilidad de que ambos sean niños, condicionada porque el segundo sea niño?
b) ¿Cuál es la probabilidad de que ambos sean niños, condicionada porque al menos uno sea niño?
Definiendo las variables se tiene
\(A_n\equiv\) nace el niño n-ésimo
\(B_n\equiv\) nace la niña n-ésima
a) Para estudiar la probabilidad condicionada pedida, consultar la teoría de probabilidad condicionada,
\(P(A_1\cap A_2|A_2)=\frac{P(A_1\cap A_2)\cap A_2}{P(A_2)}=\frac{P(A_1\cap A_2)}{P((A_1\cap A_2)\cup (B_1\cap A_2))}=\frac{P(A_1)P(A_2)}{P(A_1\cap A_2)+P(B_1\cap A_2)}\)
\(P(A_1\cap A_2|A_2)=\frac{P(A_1)P(A_2)}{P(A_1)P(A_2)+P(B_1)P(A_2)}=\frac{0,51.0,51}{0,51.0,51+0,49.0,51}=\bbox[yellow]{0,51}\)
b) En este segundo caso también se trata de una probabilidad condicionada
\(P(A_1\cap A_2|A_1\cup A_2)=\frac{P(A_1\cap A_2)\cap (A_1\cup A_2)}{P(A_1\cup A_2)}=\frac{P(A_1\cap A_2)}{P(\bar{B_1\cap B_2})}=\frac{P(A_1)P(A_2)}{1-P(B_1\cap B_2)}\)
\(P(A_1\cap A_2|A_1\cup A_2)=\frac{P(A_1)P(A_2)}{1-P(B_1)P(B_2)}=\frac{0,51.0,51}{1-0,49.0,49}=\bbox[yellow]{0,34}\)
\[\]Ejercicio 4: (2 ptos) Se supone que la presión diastólica en una determinada población se puede aproximar por una variable aleatoria con distribución normal de media \(98\)mm y desviación típica \(15\) mm. Se toma una muestra aleatoria simple de tamaño \(9\)
a) Calcúlese la probabilidad de que la media muestral sea mayor que \(100\) mm
b) Si se sabe que la media muestral es mayor que \(100\) mm, ¿cuál es la probabilidad de que sea también menor que \(104\) mm?
a) Por los datos del enunciado, siendo \(x\) la variable que mide la presión diastólica, ésta seguirá una normal de la forma \(x\equiv N(98, 15)\), ver estadística
Las medias de muestras aleatorias de nueve elementos también seguirá una distribución Normal: \(\bar{x}:N(98,\frac{15}{\sqrt{5}})=N(98,5)\)
El ejercicio pide hallar la probabilidad de que la media sea superior a \(100\), es decir, \(P(\bar{x}>100)\), para poder utilizar la tabla de la normal, ha de normalizarse la variable \(X\) (ya que la tabla es para variables que siguen una \(N(0,1)\), consultar teoría de estadística)
De forma que \(z=\frac{\bar{x}-\mu}{\sigma}\) y
\(P(\bar{x}>100)=P(z>\frac{100-9,8}{5})=P(z>0,40)=1-P(z<0,40)\)
Consultando la tabla de la normal se tiene el resultado pedido, \(\bbox[yellow]{P(\bar{x}>100)=0,3446}\)
b) Se pide hallar una probabilidad condicionada, ver teoría sobre la probabilidad condicionada
\(P(\bar{x}<104|\bar{x}>100)=\frac{P(100<\bar{x}<104)}{P(\bar{x}>100)}\)
Por una parte y normalizando la variable se tiene, ver cómo tipificar una variable aleatoria y consultar la tabla de la normal
\(P(100<\bar{x}<104)=P(\frac{100-98}{5}<\bar{x}<\frac{104-98}{5})\)
Por lo tanto, \(P(0,40<z<1,20)=0,8849-0,6554=0,2292\)
Del primer apartado se sabe que \(P(\bar{x}>100)=0,3446\), luego sustituyendo ambos valores en la fórmula para la probabilidad condicionada, se tiene
\(P(\bar{x}<104|\bar{x}>100)=\frac{0,2292}{0,3446}=\bbox[yellow]{0,6551}\)
Ir a la Opción B de este examen