OPCIÓN B
\[\]Ejercicio 1: (2 ptos) Se considera el sistema lineal de ecuaciones dependientes del parámetro real \(k\):
\(\displaystyle\begin{cases}kx+y=0&\\x+ky-2z=1& \\kx-3y+kz=0&\\\end{cases}\)
a) Discútase el sistema según los diferentes valores de \(k\)
b) Resuélvase el sistema en el caso \(k=1\)
a) Para discutir el sistema de ecuaciones, se calcula el rango de la matriz asociada al sistema así como el rango de la matriz ampliada, consultar el estudio de un sistema de ecuaciones a través del rango de la matriz asociada
\(A=\begin{pmatrix}k &1&0\\ 1&k& -2\\ k&-3& k\end{pmatrix}\) y \(A^{*}=\begin{pmatrix}k &1&0&0\\ 1&k& -2&1\\ k&-3& k&0\end{pmatrix}\)
El rango de \(A\) y de \(A^{*}\) no puede ser mayor que tres
Recordando cómo se resuelven determinantes, se tiene \(|A|=k^3-2k+0-(0+k+6k)=k^3-9k=0\Rightarrow k=0\), \(k=-3\) y \(k=3\)
– Si \(k\neq 0,\pm 3\), \(|A|\neq 0\Rightarrow\hbox{El rango de }A=\hbox{ el rango de }A^{*}=3=\hbox{n. de variables en el sistema}\Rightarrow\bbox[yellow]{\hbox{el sistema es compatible determinado si }k\neq 0,\pm 3}\)
– Si \(k=0\), \(|A|=0\). Encontrando además el menor tal que \(\begin{array}{|crl|}0 &1\\ 1& 0\end{array}=-1\neq 0\Rightarrow A\hbox{ tiene rango }2\)
En la matriz \(A^{*}\) todos los menores tres por tres tienen determinante nulo, luego, su rango será también dos
Por lo tanto, \(\hbox{ el rango de }A =\hbox{ rango de }A^{*}\Rightarrow\bbox[yellow]{\hbox{si }k=0,\hbox{El sistema es compatible indeterminado}}\)
– Si \(k=3\), \(|A|=0\) y, al igual que en el caso anterior, se encuentra un menor tal que \(\begin{array}{|crl|}3 &1\\ 1& 3\end{array}=8\neq 0\Rightarrow A\hbox{ tiene rango }2\)
En \(A^{*}\) se encuentra el menor \(3\times 3\) tal que
\(\begin{array}{|crl|}3 &1&0\\ 1& 3&1\\ 3& -3&0\end{array}\neq 0\Rightarrow A^{*}\hbox{ tiene rango }3\)
Por lo tanto, se concluye en este caso que \(\hbox{ el rango de }A \neq\hbox{ rango de }A^{*}\Rightarrow\bbox[yellow]{\hbox{si }k=3,\hbox{El sistema es incompatible}}\)
– Si \(k=-3\), el determinante de \(A\) es nulo y se tiene el menor
\(\begin{array}{|crl|}-3 &1\\ 1& -3\end{array}=8\neq 0\Rightarrow A\hbox{ tiene rango }2\)
Como en el caso \(k=3\), se encuentra en la matriz ampliada un menor tres por tres tal que
\(\begin{array}{|crl|}-3 &1&0\\ 1& -3&1\\ -3& -3&0\end{array}\neq 0\Rightarrow A^{*}\hbox{ tiene rango }3\)
Por lo tanto, se concluye en este caso que \(\hbox{ el rango de }A \neq\hbox{ rango de }A^{*}\Rightarrow\bbox[yellow]{\hbox{si }k=-3,\hbox{El sistema es incompatible}}\)
b) Para \(k=1\), el sistema es compatible determinado (con \(|A|=k^3-9k=-8\)) y se puede resolver por el método de Cramer. Para ello se considera el determinante de \(A\) y los siguientes determinantes, ver la Regla de Cramer,
\(|A_x|=\begin{array}{|crl|}0 & 1 & 0 \\1 & 1 & -2\\0 & -3 &1\end{array}=-1\)
\(|A_y|=\begin{array}{|crl|}1 & 0 & 0 \\1 & 1 & -2\\1 & 0 &1\end{array}=1\)
\(|A_z|=\begin{array}{|crl|}1 & 1 & 0 \\1 & 1 & 1\\1 & -3 &0\end{array}=4\)
Por lo que la solución será \((x,y,z)=(\frac{|A_x|}{|A|},\frac{|A_y|}{|A|},\frac{|A_z|}{|A|})=\bbox[yellow]{(\frac 18,-\frac 18,-\frac 12)}\)
Ejercicio 2: (2 ptos) Se considera la función real de variable real definida por:
\(f(x)=\displaystyle\begin{cases}ax^2-3&x\leq 1\\ \ln (2x-1)&x>1\\\end{cases}\)
a) (1 pto) Calcúlese el valor de \(a\) para que la función sea continua en todo \(\mathbb{R}\)
b) (1 pto) Represéntese gráficamente la función para el caso \(a=3\)
a) La función está formada por un polinomio y un logaritmo que es continuo en su dominio (en el intervalo donde está definido), luego el único punto de posible discontinuidad es el salto entre los polinomios, es decir, \(x=1\) (ver continuidad de funciones)
Para comprobar si la función es continua en dicho punto se evalúan los límites laterales y la función en el punto
\(\lim\limits_{x\to 1^{+}}f(x)=\lim\limits_{x\to 1^{+}}\ln (2x-1)=\ln (2.1-1)=\ln 1=0\)
Calculando el otro límite lateral, se tiene
\(\lim\limits_{x\to 1^{-}}f(x)=\lim\limits_{x\to 1^{-}}ax^2-3=a.1^2-3=a-3=f(1)\)
Luego, para que la función sea continua en \(1\) (y, por tanto, en todo \(\mathbb{R}\)), se debe cumplir que \(a-3=0\Rightarrow\bbox[yellow]{a=3}\)
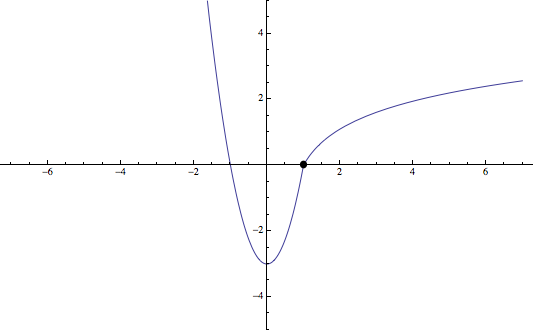
b) La función que se pide representar en el enunciado es la siguiente
\(f(x)=\displaystyle\begin{cases}3x^2-3&x\leq 1\\ \ln (2x-1)&x>1\\\end{cases}\)
Para representar la función se seguirán los pasos para dibujar el gráfico de una función
– El dominio en este caso serán todos los números reales, ver dominio de una función
– Para calcular el corte con los ejes se iguala la función a cero, ver cómo obtener los cortes con los ejes
\(f(x)=0\Rightarrow 3x^2-3=0\) y \(\ln (2x-1)=0\Rightarrow x=\pm 1\), luego los puntos de corte hallados serán \((-1,0)\) y \((1,0)\)
Por otra parte, evaluando \(f(0)\) se tiene \(f(0)=3.0^2-3=-3\), luego otro punto de corte será \((0,-3)\)
Con estos datos y sabiendo que \(3x^2-3\) es una parábola trasladada (y su vértice estará en \((0,-3)\)), ver funciones elementales, es posible dibujar la función
\[\] Ejercicio 3: (2 ptos) Dada la función \(f(x)=\frac{x}{x^2+4}\)
a) (1 pto) Determínense los extremos relativos de \(f(x)\)
b) (1 pto) Calcúlese la integral definida \(\displaystyle\int_0^1f(x)dx\)
a) Para calcular los máximos y mínimos de la función (extremos relativos) se derivará la función y se igualará a cero, ver máximos y mínimos y la tabla de derivadas
\(f'(x)=\frac{1.(x^2+4)-x.2x}{(x^2+4)^2}=0\Rightarrow \frac{4-x^2}{(x^2+4)^2}=0\Rightarrow 4-x^2=0\Rightarrow x=\pm 2\)
Para saber si los puntos críticos obtenidos son máximos o mínimos, se evalúas en la segunda derivada y se estudia el signo de la misma,
\(f»(x)=\frac{-2x(x^2+4)^2-(4-x^2)2(x^2+4)2x}{(x^2+4)^4}=\frac{2x^3-24x}{(x^2+4)^3}\)
Sustituyendo los valores obtenidos, \(x=\pm 2\), se tiene que
\(f»(-2)=\frac{32}{512}>0\) y \(f»(2)=-\frac{32}{512}<0\)
De esta forma, consultando cómo saber si los puntos críticos son máximos o mínimos, se concluye que (sabiendo que \(f(-2)=-\frac 14\) y que \(f(2)=\frac 14\)) la función tiene:
\(\bbox[yellow]{\hbox{max. en }(2,\frac 14)\hbox{ y min. en }(-2,-\frac 14)}\)
b) Para calcular la integral pedida recordar cómo se calcula una integral definida y la tabla de integrales y las propiedades de los logaritmos
\(\displaystyle\int_0^1f(x)dx=\int_0^1\frac{x}{x^2+4}dx=\frac 12\int_0^1\frac{2x}{x^2+4}dx=\frac 12\ln (x^2+4)\Big]_0^1=\frac 12\ln (1^2+4)-\frac 12\ln (0^2+4)=\bbox[yellow]{\ln\frac{\sqrt{5}}{2}}\)
\[\]Ejercicio 4: (2 ptos) Una caja de caramelos contiene \(7\) caramelos de menta y \(10\) de fresa. Se extrae al azar un caramelo y se sustituye por dos del otro sabor. A continuación se extrae un segundo caramelo. Hállase la probabilidad de que:
a) El segundo caramelo sea de fresa
b) El segundo caramelo sea del mismos abor que el primero
a) Para resolver el problema se definen las variables a utilizar:
\(M_i\equiv\) Extraer un caramelo de menta en la extracción i
\(F_i\equiv\) Extraer un caramelo de fresa en la extracción i
Los datos que da el enunciado son los siguientes
\(P(M_i)=\frac{7}{17}\)
\(P(F_i)=\frac{10}{17}\)
\(P(M_2|M_1)=\frac{6}{18}=\frac 13\)
\(P(F_2|M_1)=\frac{12}{18}=\frac 23\)
\(P(M_2|F_1)=\frac{9}{18}=\frac 12\)
\(P(F_2|F_1)=\frac{9}{18}=\frac 12\)
a) La probabilidad de que el segundo caramelo sea de fresa (\(F_2\)), será la probabilidad de que el segundo caramelo sea de fresa habiendo sido el primero de menta más la probabilidad de que sea de fresa el segundo habiéndose extraído primeramente otro de fresa, ver la teoría de la probabilidad
\(P(F_2)=P((M_1\cap F_2)\cup (F_1\cap F_2))=P(M_1\cap F_2)+P(F_1\cap F_2)=P(M_1)P(F_2|M_1)+P(F_1)P(F_2|F_1)\)
Luego, \(P(F_2)=\frac{7}{17}\frac 23+\frac{10}{17}\frac 12=\bbox[yellow]{\frac{29}{51}}\)
b) La probabilidad de que el segundo caramelo sea del mismo sabor que el primero será la suma de las probabilidades de que el primero sea de menta y el segundo también y la de que ambos sean de fresa
\(P((M_1\cap M_2)\cup (F_1\cap F_2))=P(M_1\cap M_2)+P(F_1\cap F_2)=P(M_1)P(M_2|M_1)+P(F_1)P(F_2|F_1)\)
Luego, \(P((M_1\cap M_2)\cup (F_1\cap F_2))=\frac{7}{17}\frac 13+\frac{10}{17}\frac 12=\bbox[yellow]{\frac{22}{51}}\)
\[\]Ejercicio 5: (2 ptos) Se considera una variable aleatoria con distribución normal de media \(\mu\) y desviación típica igual a \(210\). Se toma una muestra aleatoria simple de \(64\) elementos
a) Calcúlese la probabilidad de que el valor absoluto de la diferencia entre la media muestral y \(\mu\) sea mayor o igual que \(22\)
b) Determínese un intervalo de confianza del \(99\)% para \(\mu\), si la media muestral es igual a \(1532\)
a) Por los datos del enunciado, siendo \(x\) la variable dada, seguirá una normal de la forma \(X\equiv N(\mu, \sigma)\), ver estadística
Para muestras de tamaño \(64\) elementos, se tendrán las medias muestrales que seguirán una distribución Normal: \(\bar{x}:N(\mu,\frac{\sigma}{\sqrt{64}})\)
El ejercicio pide hallar \(P(|\bar{x}-\mu|\geq 22)\)
Es decir, \(P(|\bar{x}-\mu|\geq 22)=1-P(|\bar{x}-\mu|< 22)=1-P(-22<\bar{x}-\mu< 22)=1-P(\mu-22<\bar{x}< \mu +22)\)
Para poder utilizar la tabla de la normal, ha de normalizarse la variable \(\bar{x}\) (ya que la tabla es para variables que siguen una \(N(0,1)\), consultar teoría de estadística)
De forma que \(z=\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{64}}}\) y
\(1-P(\mu-22<\bar{x}< \mu +22)=1-P(\frac{\mu-22-\mu}{\frac{210}{8}}<z<\frac{\mu+22-\mu}{\frac{210}{8}})=1-P(-0,84<z<0,84)=1-(P(z<0,84)-P(z\leq -0,84))=1-(P(z<0,84)-P(z\geq 0,84))=1-(P(z<0,84)-(1-P(z< 0,84))\)
Consultando la tabla de la normal se tiene el resultado pedido, \(\bbox[yellow]{P(|\bar{x}-\mu|\geq 22)=0,401}\)
b) El intervalo de confianza se hallará con la siguiente fórmula, ver teoría de estadística,
\(IC=(\bar{x}-z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}},\bar{x}+z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}})\)
El valor de \(z_{\frac{\alpha}{2}}\) se obtiene a partir del nivel de confianza dado en el enunciado
Nivel de confianza del \(99\hbox{%}\Rightarrow 1-\alpha=0,99\Rightarrow \alpha=0,01\Rightarrow z_{\frac{\alpha}{2}}=2,58\)
Por lo tanto,
\(IC=(1532-2,58\frac{210}{\sqrt{64}},1532+2,58\frac{210}{\sqrt{64}})=\bbox[yellow]{(1464, 1600)}\)