Ejercicio : (Septiembre 2014 Opción A)(Calificación: 2 ptos) Se considera la función real de variable real definida por \(\frac{(x-3)^2}{x(x-2)}\)
1. Determínense las asíntotas de \(f\)
2. Estúdiese si la función \(f\) es creciente o decreciente en un entorno de \(x = 4\)
1. Para estudiar las asintótas de la función conviene consultar el apartado de teoría de asíntotas
. Asíntotas verticales:
Las posibles asíntotas verticales estarían en los puntos que no están en el dominio, ver cómo se calcula el dominio de una función. En este caso, los únicos puntos reales en los que no está definida la función son \(0 y 2\)
Para comprobar si en esos puntos hay asíntotas se calculan los límites laterales de la función.
\(\lim\limits_{x\to 2^{-}}\frac{(x-3)^2}{x(x-2)}=-\infty\)
\(\lim\limits_{x\to 2^{+}}\frac{(x-3)^2}{x(x-2)}=\infty\)
y
\(\lim\limits_{x\to 0^{-}}\frac{(x-3)^2}{x(x-2)}=\infty\)
\(\lim\limits_{x\to 0^{+}}\frac{(x-3)^2}{x(x-2)}=-\infty\)
Luego, hay asíntotas verticales en \(\bbox[yellow]{x=0, x=2}\)
. Asíntotas horizontales:
\(\lim\limits_{x\to\pm\infty}f(x)=1\), luego hay una asíntota horizontal en \(\bbox[yellow]{y=1}\)
. Asíntotas oblicuas:
Como hay asíntotas horizontales, \(\bbox[yellow]{\hbox{no hay oblicuas}}\), ver la teoría de asíntotas
2. Los intervalos de crecimiento y decrecimiento se estudiarán calculando los máximos y mínimos de la función, ver máximos y mínimos, la tabla de derivadas y consultar también cómo resolver polinomios
\(f'(x)=\frac{2(x-3)(2x-3)}{x^2(x-2)^2}=0\Rightarrow x=3, x=\frac 32\)
La derivada es positiva antes del punto \(x=\frac 32\) y después del \(x=3\)
Entre \(\frac 32 y 3\), \(f'(x)\) es negativa, luego la función \(f\) crecerá en los intervalos \((-\infty, \frac 32)\cup (3,\infty)\) y decrecerá en \((\frac 32, 3)\)
Como \(x=4\) está en el intervalo \((3,\infty)\), la función será \(\bbox[yellow]{\hbox{creciente en un entorno de } x=4}\)
Ejercicio : (Septiembre 2014 Opción A)(Calificación: 2 ptos)
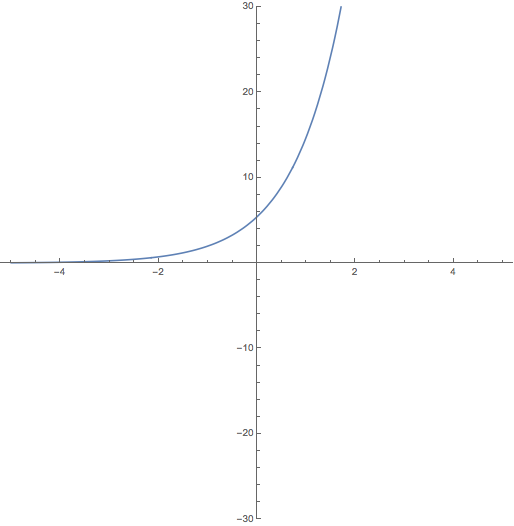
Se considera la función real de variable real definida por \(f(x) = 2e^{x+1}\)
1. Esbócese la gráfica de la función \(f\)
2. Calcúlese el área del recinto plano acotado limitado por la gráfica de
la función, el eje de abscisas y las rectas \(x = 0\) y \(x = 1\)
Para representar la función se seguirán los pasos para dibujar el gráfico de una función
– El dominio de la función serán todos los números reales, ver cómo calcular el dominio de una función
– Para calcular el corte con los ejes se iguala la función a cero y se iguala también \(x\) a cero, ver cómo obtener los cortes con los ejes
\(f(x)=0\Rightarrow 2e^{x+1}=0\Rightarrow\hbox{Imposible}\) y \(f(0)=2e\), luego los cortes con los ejes serán \((0,2e)\)
– Para estudiar las asíntotas de la función consultar asíntotas y ver cómo resolver límites
. Asíntotas verticales: No hay ya que no hay puntos fuera del dominio de \(f(x)\)
. Asíntotas horizontales:
\(\lim\limits_{x\to\pm\infty}2e^{x+1}=+\infty\), luego no hay asíntotas verticales y tampoco oblicuas
– Los intervalos de crecimiento y decrecimiento se estudian calculando los máximos y mínimos de \(f(x)\), ver máximos y mínimos y la tabla de derivadas
\(f'(x)=2e^{x+1}=0\Rightarrow \hbox{Imposible porque}2e^{x+1}>0\), luego la función es siempre creciente
– Para estudiar la curvatura de la función se hallan los puntos de inflexión de \(f(x)\), ver cómo estudiar la curvatura de una función
\(f»(x)=2e^{x+1}=0\Rightarrow \hbox{Imposible porque}2e^{x+1}>0\), luego la función no cambia su curvatura
Así que la gráfica de la función será
2. Para hallar el área pedida y teniendo en cuenta la gráfica de la función \(f(x)\), ver funciones elementales, se evaluará la integral de la función entre \(0\) y \(1\), ver cómo se calcula una integral definida y consultar también la tabla de integrales
\(\displaystyle A=\int_0^{1}2e^{x+1}dx=2e^{x+1}\Big]_{0}^{1}=\bbox[yellow]{2e(e-1)}\)
Ejercicio :(Septiembre 2014 Opción B)(Calificación: 2 ptos)
Se considera la función real de variable real definida por \(f(x)= \frac{\lambda x}{4+x^2}\)
1. Calcúlese el valor del parámetro real \(\lambda\) para que la recta tangente a la gráfica de f en \(x=-1\) sea paralela a la recta \(y=2x-3\)
2. Calcúlese \(\int_0^2 f(x)dx\) para \(\lambda = 1\)
1. Para que la recta tangente a \(f\) sea paralela a \(y=2x−3\) su pendiente tiene que ser la misma, ver condición rectas paralelas y ver también pendiente de una recta
\(f'(x)=\frac{\lambda(4-x^2)}{(x^2+4)^2}\) y se tiene que cumplir que \(f'(-1)=2\), por lo tanto, \(\lambda=\frac{50}{3}\)
2. Para calcular la integral pedida recordar la teoría sobre cálculo de integrales y la tabla de integrales,
\(\int_0^2 f(x)dx=\int_0^2 \frac{x}{4+x^2}dx=\frac 12\ln |4+x^2| \Big|_0^2=\bbox[yellow]{\frac{\ln 2}{2}}\)