OPCIÓN B
\[\]Ejercicio 1: (3 ptos) Dada la función \(f(x)=\frac{ax^4+1}{x^3}\)
a) (1 pto)Determinar el valor de \(a\)para el que la función posee un mínimo relativo en \(x=1\). Para ese valor de \(a\), obtener los otros puntos en que \(f\) tiene un extremo relativo
b) (1 pto) Obtener las asíntotas de la gráfica de \(y=f(x)\) para \(a=1\)
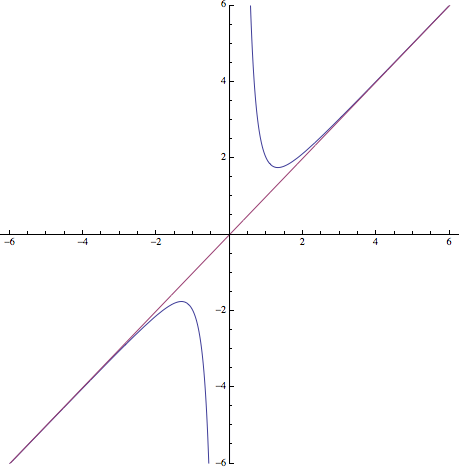
c) (1 pto) Esbozar la gráfica de la función para \(a=1\)
a) Para que la función tenga un mínimo en \(x=1\), tiene que cumplirse que la derivada en ese punto sea cero, ver máximos y mínimos y consultar también la tabla de derivadas
\(f'(x)=\frac{4ax^3.x^3-(ax^4+1)3x^2}{(x^3)^2}\Rightarrow \frac{4ax^4-3ax^4-3}{x^4}\Rightarrow \frac{ax^4-3}{x^4}\Rightarrow f'(1)=\frac{a-3}{1}=0\Rightarrow a=3\)
Para saber si con ese valor de \(a\), \(x=1\) es un mínimo, se evalúa \(x=1\) en la segunda derivada,
\(f»(x)=\frac{12x^3.x^4-(3x^4-3)4x^3}{(x^4)^2}=\frac{12}{x^5}\)
Sustituyendo \(x=1\), se tiene que \(f»(1)=12>0\). Luego, en \(x=1\) hay, efectivamente, un mínimo y, por lo tanto, el resultado será \(\bbox[yellow]{a=3}\)
b) Para estudiar las asintótas de la función, consultar el apartado de teoría de asíntotas
. Asintótas verticales:
Las posibles asíntotas verticales estarían en los puntos que no están en el dominio, ver cómo se calcula el dominio de una función. En este caso, el denominador se anula en \(x=0\) y consultando cómo resolver límites, se tiene
\(\lim\limits_{x\to 0^{-}}\frac{x^4+1}{x^3}=-\infty\)
\(\lim\limits_{x\to 0^{+}}\frac{x^4+1}{x^3}=\infty\)
Luego, hay una asíntota vertical en \(\bbox[yellow]{x=0}\)
. Asintótas horizontales:
Consultando cómo se resuelven límites se tiene que
\(\lim\limits_{x\to\pm\infty}\frac{x^4+1}{x^3}=\infty\)
Luego, \(\bbox[yellow]{\hbox{no hay horizontales}}\)
. Asintótas oblicuas:
Las posibles asíntotas oblicuas tendrían la siguiente expresión \(y=mx+n\)
Con \(m=\lim\limits_{x\to\pm\infty}\frac{f(x)}{x}=\lim\limits_{x\to\pm\infty}\frac{\frac{x^4+1}{x^3}}{x}=1\)
Y \(n=\lim\limits_{x\to\pm\infty}(f(x)-mx)=\lim\limits_{x\to\pm\infty}(\frac{x^4+1}{x^3}-x)=\lim\limits_{x\to\pm\infty}\frac{x^4+1-x^4}{x^3}=\lim\limits_{x\to\pm\infty}\frac{1}{x^3}=0\)
Luego, la recta \(\bbox[yellow]{y=x}\) será asíntota oblicua
c) Para representar la función se seguirán los pasos para dibujar el gráfico de una función
– El dominio en este caso serán todos los números reales menos el cero ya que el denominador sólo se anula en este valor, ver dominio de una función
– Para calcular el corte con los ejes se iguala la función a cero, ver cómo obtener los cortes con los ejes
\(f(x)=0\Rightarrow x=\pm (-1)^{\frac 14}\Rightarrow\hbox{Imposible}\), luego la función no cortará a \(y=0\)
Por otra parte, como el cero no está en el dominio, la función tampoco cortará a \(x=0\)
Con estos datos y los obtenidos en los apartados anteriores, es posible dibujar la función
Ejercicio 2: (3 ptos)
a) (2 ptos) Discutir el sistema de ecuaciones \(AX=B\), donde
\(A=\begin{pmatrix}0&1&m-1\\ 0&m-1&1\\ m-2&0&0\end{pmatrix}\), \(X=\begin{pmatrix}x\\ y\\z\end{pmatrix}\), \(B=\begin{pmatrix}m\\ m\\ m+2\end{pmatrix}\)
según los valores de \(m\)
b) (1 pto) Resolver el sistema en los casos \(m=0\) y \(m=1\)
a) La matriz ampliada del problema será \(A^{*}=\begin{pmatrix}0&1&m-1&m\\ 0&m-1&1&m\\ m-2&0&0&m+2\end{pmatrix}\)
Ambas matrices tienen tres filas, luego, como máximo el rango será tres, ver rango de matrices
Calculando el determinante de \(A\) se tiene, ver cómo resolver determinantes, \(\begin{array}{|crl|}0 & 1 & m-1\\0 & m-1 & 1\\m-2 & 0 & 0\end{array}=-m(m-2)^2=0\Rightarrow -m(m-2)^2\Rightarrow m=0\) y \(m=2\)
– Si \(m\neq 0,2\), el determinante de \(|A|\) es distinto de cero, por lo tanto ,\(\hbox{el rango de }A\hbox{ es igual al }\hbox{rango de }A^{*}=3\Rightarrow\bbox[yellow]{\hbox{si } m\neq -1,2,\hbox{ el sistema es compatible determinado}}\)
– Si \(m=0\), matriz \(A\) tiene determinante nulo y todos los menores tres por tres de \(A^{*}\) también tienen determinante nulo, ver cómo resolver determinantes, por lo tanto, como tanto en \(A\) como en \(A^{*}\) existe el menor
\(\begin{array}{|crl|}0& -1\\-2 & 0\end{array}=-2\neq 0\)
\(\hbox{si } m=0,\hbox{el rango de }A\hbox{ es }\hbox{ es igual al }\hbox{rango de }A^{*}=2\Rightarrow\bbox[yellow]{\hbox{si } m=0 \hbox{ el sistema es compatible indeterminado}}\)
– Si \(m=2\), \(A\) será \(A=\begin{pmatrix}0 &1&1\\ 0&1&1\\ 0&0&0\end{pmatrix}\)
Todos los menores de esa matriz de orden tres y de orden dos son nulos. Por otra parte, en \(A^{*}\) es posible encontrar el siguiente menor \(\begin{array}{|crl|}1& 2\\0 & 4\end{array}=4\neq 0\) por lo
tanto \(\hbox{si } m=2,\hbox{el rango de }A\hbox{ es }\hbox{ es distinto al }\hbox{rango de }A^{*}\Rightarrow\bbox[yellow]{\hbox{si } m=2 \hbox{ el sistema es incompatible}}\)
b) Sustituyendo el valor de \(A\) cuando \(m=0\) en la ecuación matricial propuesta, se tiene el siguiente sistema, recordar cómo operar con matrices
\(\begin{cases}y-z=&0\\-y+z=&0\\-2x=&2\\\end{cases}\)
La primera y la segunda ecuación son proporcionales, de forma que basta una de ellas (y la tercera) para resolverlo, ver cómo resolver sistemas de ecuaciones
\(\begin{cases}-y+z=&0\\-2x=&2\\\end{cases}\Rightarrow\bbox[yellow]{\begin{cases}x=&-1\\y=&\lambda\\z=&\lambda\\\end{cases}}\)
En el caso de \(m=1\) el sistema será compatible determinado y se obtendrá
\(\begin{cases}-y=&1\\z=&1\\-x=&3\\\end{cases}\Rightarrow\bbox[yellow]{\begin{cases}x=&-3\\y=&1\\z=&1\\\end{cases}}\)
\[\] Ejercicio 3: (2 ptos) Dados los planos
\(\pi_1\equiv 2x+y-2z=1\;\;\), \(\;\pi_2\equiv x-y+2z=1\)
se pide:
a) (0,5 ptos) Estudiar su posición relativa
b) (1,5 ptos) En caso de que los planos sean paralelos, hallar la distancia entre ellos; en caso de que se corten, hallar un punto y un vector de dirección de la recta que determinan
a)Si dos de los coeficientes de la ecuación general de ambos planos no son proporcionales (mirando la proporción entre coordenada y coordenada), los planos serán secantes, ver posición relativa entre dos planos
En este caso, \(\frac{2}{1}\neq\frac{1}{-1}=\frac{-2}{2}\Rightarrow\bbox[yellow]{\hbox{Los planos son secantes}}\)
b) Las ecuaciones paramétricas de la recta que determinarán los dos planos dados se obtendrán resolviendo el sistema siguiente, ver resolución de sistemas de ecuaciones
\(\bbox[yellow]{r:\begin{cases}2x+y-2z=&1\\x-y+2z=&1\\\end{cases}\Rightarrow\begin{cases}x=&\frac 23\\y=&\frac 13+2\lambda\\z=&\lambda\\\end{cases}}\)
El vector director de la recta será \(\bbox[yellow]{\vec{v}=(0,2,1)}\), ver cómo hallar un vector director de una recta dada, y un punto de dicha recta será \(\bbox[yellow]{P(\frac 23,\frac 13,0)}\)
\[\]Ejercicio 4: (2 ptos)
a) (0,75 ptos) Hallar la ecuación del plano \(\pi_1\) que pasa por los puntos \(A(1,0,0)\), \(B(0,2,0)\) y \(C(0,0,1)\)
b) (0,75 ptos) Hallar la ecuación del plano \(\pi_2\) que contiene al punto \(P(1,2,3)\) y es perpendicular al vector \(\vec{v}=(-2,1,1)\)
c) (0,5 ptos) Hallar el volumen del tetraedro de vértices \(A,B,C\) y \(P\)
a) Con los tres puntos dados es posible escribir la ecuación del plano pedido, ver cómo se construye un plano
\(\pi_2\equiv\frac x1+\frac y2+\frac z1=1\Rightarrow\bbox[yellow]{\pi_1\equiv 2x+y+2z-2=0}\)
b) El vector \(\vec{v}\) dado será el vector normal del plano pedido, luego su ecuación vendrá dada por, ver de nuevo cómo se construye un plano
\(\pi_2\equiv -2x+y+z+C=0\)
La constante \(C\) se obtiene sustituyendo el punto \(P\) en la ecuación del plano (ya que el enunciado dice que dicho punto pasa por el plano), es decir
\(-2.1+2+3+C=0\Rightarrow C=-3\Rightarrow\bbox[yellow]{\pi_2\equiv-2x+y+z-3=0}\)
c) El volumen de un tetraedro se calcula utilizando la siguiente fórmula que involucra el producto mixto entre vectores, ver cómo hallar el volumen de un tetraedro
\(V=\frac 16|\vec{AP}(\vec{BP}\times\vec{CP})|\)
Calculando término a término, se tiene
\(\vec{AP}=(0,2,3)\), \(\vec{BP}=(1,0,3)\) y \(\vec{CP}=(1,2,2)\)
De esta forma, resolviendo un determinante se obtiene el resultado final, ver cómo resolver determinantes
\(V=\frac 16\begin{array}{|crl|}0 &2&3\\ 1&0&3\\ 1&2&2\end{array}=\frac 86=\bbox[yellow]{\frac 43}\)