OPCIÓN B

\[\]Ejercicio 1: (3 ptos) Sean \(r_A\) la recta con vector dirección \((1,\lambda,2)\) que pasa por el punto \(A(1,2,1)\), \(r_B\) la recta con vector dirección \((1,1,1)\) que pasa por \(B(1,-2,3)\), y \(r_C\) la recta con vector dirección \((1,1,-2)\) que pasa por \(C(4,1,-3)\). Se pide:

a) (1 pto) Hallar \(\lambda\) para que las rectas \(r_A\) y \(r_B\) se corten
b) (1,5 ptos) Hallar \(\lambda\) para que a recta \(r_A\) sea paralela al plano definido por \(r_B\) y \(r_C\)
c) (0,5 ptos) Hallar el ángulo que forman \(r_B\) y \(r_C\)

a) Para que dos rectas se corten, el rango de la matriz de los vectores directores de ambas rectas y el vector formado por un punto de cada recta debe ser dos, ver posiciones relativas entre dos rectas

En este caso,

\(r_A:\begin{cases}A&(1,2,1)\\\vec{v_A}=&(1,\lambda,2)\\\end{cases}\) \(r_B:\begin{cases}B&(1,-2,3)\\\vec{v_A}=&(1,1,1)\\\end{cases}\) y \(r_C:\begin{cases}C&(4,1,-3)\\\vec{v_C}=&(1,1,-2)\\\end{cases}\)

Y además \(\vec{AB}=(1,-2,3)-(1,2,1)=(0,-4,2)\)

De forma que el determinante a estudiar será, ver cómo resolver determinantes

\(\begin{array}{|crl|}1 & \lambda & 2\\1 & 1 & 1\\0 & -4 & 2\end{array}=2+0-8-(0+2\lambda -4)=-2\lambda -2=0\Rightarrow \bbox[yellow]{\lambda=-1}\)

. Si \(\lambda\neq -1\), el determinante será distinto de cero y, por lo tanto, el rango de la matriz será tres y las rectas se cruzan, ver posiciones relativas entre dos rectas

. Si \(\lambda =-1\), el rango es dos y las rectas se cortan

b) Para que la recta \(r_A\) sea paralela al plano, \(\pi\) que definen \(r_B\) y \(r_C\), el vector director \(\vec{v_A}\) debe ser perpendicular al vector del plano determinado por \(r_B\) y \(r_C\), ver

Primeramente se halla el plano \(\pi\), para calcular el vector característico, \(\vec{n_{\pi}}\), de dicho plano, se toman los vectores directores \(\vec{v_B}\) y \(\vec{v_C}\) y se calcula su producto vectorial, ver cómo calcular un plano con dos rectas dadas y ver cómo calcular el producto vectorial entre dos vectores dados

\(\vec{n_{\pi}}=\vec{r_B}\times\vec{r_C}=\begin{array}{|crl|}\vec{i} & \vec{j} & \vec{k}\\1 & 1 & 1\\1 & 1 & -2\end{array}=(-3,3-0)\)

Como lo que se pretende es que el vector obtenido, \(\vec{n_{\pi}}\), sea perpendicular al vector \(\vec{r_A}\), se tiene que, ver cómo comprobar que dos vectores son perpendiculares entre sí,

\((1,\lambda,2).(-3,3,0)=0\Rightarrow\bbox[yellow]{\lambda =1}\)

c) El ángulo formado por dos rectas viene dado por la fórmula siguiente, ver cómo calcular el ángulo formado por dos rectas,

\(\cos\alpha=\frac{\vec{v_B}.\vec{v_C}}{|\vec{v_B}||\vec{v_C}|}=\frac{1.1+1.1+1.(-2)}{\sqrt{3}\sqrt{6}}=\frac{0}{\sqrt{18}}=0\Rightarrow\bbox[yellow]{\alpha=90}\)

Ejercicio 2: (3 ptos) Dado el siguiente sistema de ecuaciones lineales:

\(\begin{cases}2x+\lambda y+\lambda z=&1-\lambda\\x+y+(\lambda -1)z=&-2\lambda \\ (\lambda -1)x+y+z=&\lambda -1\\\end{cases}\)

se pide:

a) (2 ptos) Discutirlo según los valores del parámetro \(\lambda\)
b) (0,5 ptos) Resolverlo en el caso \(\lambda=1\)
c) (0,5 ptos) Resolverlo en el caso \(\lambda=-1\)

a) Para discutir el sistema de ecuaciones, se calcula el rango de la matriz asociada al sistema así como el rango de la matriz ampliada, consultar el estudio de un sistema de ecuaciones a través del rango de la matriz asociada

\(A=\begin{pmatrix}2 &\lambda&\lambda\\ 1&1& \lambda -1\\ \lambda -1&1&1\end{pmatrix}\) y \(A^{*}=\begin{pmatrix}2 &\lambda&\lambda&1-\lambda\\ 1&1& \lambda -1&-2\lambda\\ \lambda-1&1& 1&\lambda -1\end{pmatrix}\)

El rango de \(A\) y de \(A^{*}\) no puede ser mayor que tres

Recordando cómo se resuelven determinantes, se tiene \(|A|=\lambda^3-3\lambda^2+4=0\Rightarrow \lambda=-1\) y \(\lambda=2\)

– Si \(\lambda\neq -1,2\), \(|A|\neq 0\Rightarrow\hbox{El rango de }A=\hbox{ el rango de }A^{*}=3=\hbox{n. de variables en el sistema}\Rightarrow\bbox[yellow]{\hbox{el sistema es compatible determinado si }\lambda\neq -1,2}\)

– Si \(\lambda=-1\), \(|A|=0\). Encontrando además el menor tal que \(\begin{array}{|crl|}2 &-1\\ 1& 1\end{array}=3\neq 0\Rightarrow A\hbox{tiene rango }2\)

Comprobando el determinante de \(A^{*}\) con \(\lambda=-1\) se tiene que todos los menores \(3\times 3\) tienen determinante cero, ver cómo calcular determinantes

Por lo tanto, el rango de \(A^{*}\) es también dos

De esta forma, consultando la teoría sobre estudio de rango de sistemas de ecuaciones, se tiene \(\hbox{ el rango de }A =\hbox{ rango de }A^{*}=2<3\Rightarrow\bbox[yellow]{\hbox{si }\lambda=-1,\hbox{El sistema es compatible indeterminado}}\)

– Si \(\lambda=2\), \(|A|=0\) y, al igual que en el caso anterior y la matriz queda como \(A=\begin{pmatrix}2 &2&2\\ 1&1& 1\\ 1&1&1\end{pmatrix}\) y en esta matriz sólo existen menores de orden uno distintos de cero, por lo tanto el rango de la matriz será uno

Por otra parte, en \(A^{*}\) es posible encontrar \(\begin{array}{|crl|}2 &-1\\ 1& -4\end{array}\neq 0\Rightarrow A^{*}\hbox{tiene rango }2\)

Por lo tanto, se concluye en este caso que \(\hbox{ el rango de }A \neq\hbox{ rango de }A^{*}\Rightarrow\bbox[yellow]{\hbox{si }\lambda=2,\hbox{El sistema es incompatible}}\)

b) Para \(\lambda=1\) se tiene que el sistema es: \(\displaystyle\begin{cases}2x+y+z=&0\\x+y=&-2 \\y+z=&0\\\end{cases}\)

El sistema es compatible determinado (con \(|A|=(1+1)(1-2)^2=2\)) y se puede resolver por el método de Cramer. Para ello se considera el determinante de \(A\) y los siguientes determinantes, ver la Regla de Cramer,

\(|A_x|=\begin{array}{|crl|}0 & 1 & 1 \\-2 & 1 & 0\\0 & 1 &1\end{array}=0\)

\(|A_y|=\begin{array}{|crl|}2 & 0 & 1 \\1 & -2 & 0\\0 & 0 &1\end{array}=-4\)

\(|A_z|=\begin{array}{|crl|}2 & 1 & 0 \\1 & 1 & -2\\0 & 1 &0\end{array}=4\)

Por lo que la solución será \((x,y,z)=(\frac{|A_x|}{|A|},\frac{|A_y|}{|A|},\frac{|A_z|}{|A|})=\bbox[yellow]{(0,-2,2)}\)

c) Para \(\lambda=-1\) el sistema es compatible indeterminado y quedaría como

\(\begin{cases}2x-y-z=&2\\x+y-2z=&2\\-2x+y+z=&-2\\\end{cases}\)

Como la tercera y la primera ecuación son proporcionales se puede dar el valor de un parámetro a una de las variables para resolver el sistema, ver cómo se resuelven sistemas de ecuaciones

\(\begin{cases}2x-y-z=&2\\ x+y-2z=&2\\\end{cases}\Rightarrow\begin{cases}2x-y=&2+\mu\\x+y=&2+2\mu\\\end{cases}\)

El sistema ahora se puede resolver por el método de Cramer. Para ello se considera el determinante de \(\begin{array}{|crl|}2 & -1 \\1 & 1\end{array}=3\) y los siguientes determinantes, ver cómo aplicar la Regla de Cramer,

\(|A_x|=\begin{array}{|crl|}2+\mu & -1\\2+2\mu & 1\end{array}=4+3\mu\)

\(|A_y|=\begin{array}{|crl|}2 & 2+\mu\\1 & 2+2\mu\end{array}=2+3\mu\)

Por lo que la solución será \((x,y,z)=(\frac{|A_x|}{|A|},\frac{|A_y|}{|A|},\mu)=\bbox[yellow]{(\frac 43+\mu,\frac 23 +\mu, \mu)}\)

 

\[\] Ejercicio 3: (2 ptos) Dada la función: \(\displaystyle\frac{x}{x^2+1}\), se pide:

a) (1 pto) Hallar la ecuación de la recta tangente a la gráfica de la función en el punto de abscisas \(x=0\)
b) (1 pto) Calcular \(\displaystyle\int_0^1xf(x)dx\)

a) La ecuación de la recta tangente en \(x=0\) viene dada por la siguiente ecuación, ver ecuaciones de la recta

\(y-f(0)=f'(0)(x-0)\)

Primeramente se calculará \(f(0)=\frac{0}{0^2+1}=0\) y la derivada de la función, ver la tabla de derivadas

\(f'(x)=\displaystyle\frac{1(x^2+1)-x2x}{(x^2+1)^2}\)

Luego, \(f'(0)=\frac{1-0^2}{(0^2+1)^2}=1\)

Por lo tanto, se tendrá el resultado \(y-0=(x-0)\Rightarrow\bbox[yellow]{y=x}\)

b) Consultando la tabla de integrales y recordando cómo se resuelven integrales definidas, se tiene

\(\displaystyle\int_0^1xf(x)dx=\displaystyle\int_0^1 x\frac{x}{x^2+1}dx=\displaystyle\int_0^1 \frac{x^2}{x^2+1}dx\)

Dividiendo el numerador entre el denominador, se tiene

\(\displaystyle\int_0^1 \frac{x^2}{x^2+1}dx=\displaystyle\int_0^1 (1-\frac{1}{x^2+1})dx=\displaystyle\int_0^1 1dx-\displaystyle\int_0^1\frac{1}{x^2+1}dx=x\Big]_0^1-\arctan x\Big]_0^1=\bbox[yellow]{1-\frac{\pi}{4}}\)

 

\[\]Ejercicio 4: (2 ptos) Dada la función \(f(x)=e^{\frac{1}{x}}\), se pide:

se pide:

a) (1 pto) Calcular \(\lim\limits_{x\to\infty}f(x)\), \(\lim\limits_{x\to -\infty}f(x)\) y estudiar la existencia de \(\lim\limits_{x\to 0}f(x)\)
b) (1 pto) Esbozar la gráfica \(y=f(x)\) determinando los intervalos de crecimiento y decrecimiento de \(f(x)\) y sus asíntotas

a) Para estudiar los límites, recordar la teoría de cómo resolver límites

\(\lim\limits_{x\to\infty}f(x)= \lim\limits_{x\to\infty}e^{\frac 1x}=e^{\frac{1}{\infty}}=1\) y \(\lim\limits_{x\to -\infty}f(x)= \lim\limits_{x\to -\infty}e^{\frac 1x}=e^{\frac{1}{-\infty}}=1\)

Para estudiar la existencia de \(\lim\limits_{x\to 0}f(x)\), se estudian los límites laterales y se comprueba que, si existen, son iguales, ver teoría de límites y derivabilidad

En este caso se tiene \(\lim\limits_{x\to 0^{-}}f(x)=\lim\limits_{x\to 0^{-}}e^{\frac 1x}=0\)

Por otra parte, \(\lim\limits_{x\to 0^{+}}f(x)=\lim\limits_{x\to 0^{+}}e^{\frac 1x}=\infty\)

Luego, \(\lim\limits_{x\to 0^{-}}f(x)\neq\lim\limits_{x\to 0^{+}}f(x)\Rightarrow\bbox[yellow]{\hbox{no existe }\lim\limits_{x\to 0}f(x)}\)

b) Los intervalos de crecimiento y decrecimiento se estudiarán calculando los máximos y mínimos de la función, ver máximos y mínimos y la tabla de derivadas

\(f'(x)=e^{\frac 1x}\frac{-1}{x^2}=-\frac{e^{\frac 1x}}{x^2}\neq 0\), luego, no hay puntos críticos y \(f'(x)\) es siempre menor que cero, luego la función \(\bbox[yellow]{\hbox{es decreciente en todo su dominio}}\)

Para estudiar las asintótas de la función, consultar el apartado de teoría de asíntotas

. Asintótas verticales:

Las posibles asíntotas verticales estarían en los puntos que no están en el dominio, ver cómo se calcula el dominio de una función. En este caso, el único punto real en el que no está definida la función es el cero, luego el dominio serán todos los números reales menos el cero

Para comprobar si en este punto hay asíntota se calculan los límites laterales de la función. En este caso ya se han calculado en el primer apartado, por lo que se puede concluir que la función tiene una asíntota vertical \(\bbox[yellow]{\hbox{cuando } x\hbox{ se aproxima a cero por la derecha}}\)

. Asintótas horizontales:

Consultando el apartado anterior se tiene que \(\lim\limits_{x\to\pm\infty}f(x)=1\), luego hay una asíntota horizontal en \(\bbox[yellow]{y=1}\)

. Asintótas oblicuas:

Como hay asíntotas horizontales, \(\bbox[yellow]{\hbox{no hay oblicuas}}\), ver la teoría de asíntotas

-> Para representar la función se seguirán los pasos para dibujar el gráfico de una función:

– Como ya se ha comentado, el dominio en este caso serán todos los números reales menos el cero

– Para calcular el corte con los ejes se iguala la función a cero, ver cómo obtener los cortes con los ejes

\(f(x)=0\Rightarrow \hbox{Imposible}\), luego la función no cortará a \(y=0\)

Por otra parte, como \(x=0\) no está en el dominio, no se obtiene ningún punto de corte con el eje \(OY\)

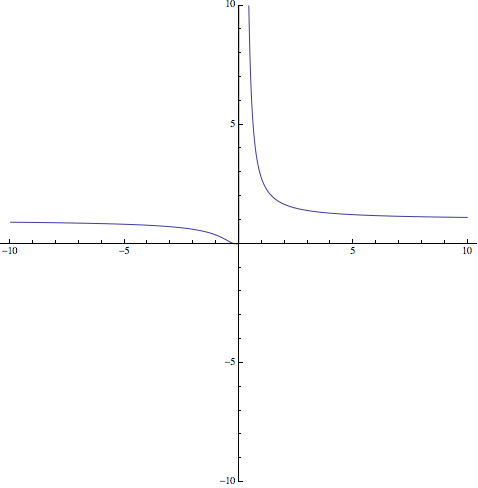
Con estos datos y los obtenidos en los apartados anteriores, es posible dibujar la función